

Ceva's Theorem is a powerful theorem in geometry, on which proofs of further theorems can utilize. For example, to prove that the three medians are concurrent is a cumbersome task, but use of Ceva's theorem greatly simplifies the proof. The proof of Ceva's theorem is usually done by constructing parallel lines and using similar triangles, but the use of ratio of areas results in a simple and easy to understand proof. This idea of using areas is obtained from Prof. J. Wilson's Homepage, where the Ceva's Theorem is presented.
In a triangle ABC, three lines from each vertex to the opposite side can be constructed. Let's label the intersection points D, E, and F as in the figure below. Then, the three lines are concurrent, that is intersect at one point, if and only if
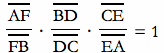
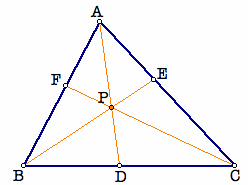
Ceva's Theorem
Consider the areas of the two triangles ABD and ACD. If we take the segments BD and DC as the base of the triangles ABD and ACD, then the two triangles will have the same height h in the calculation of their areas. Therefore, the two areas of ABD and ACD is proportional to the ratio BD : DC. That is,
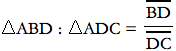
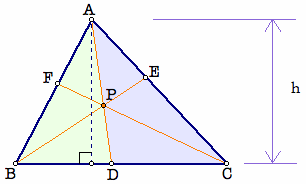
The areas of triangles ABD and ADC are proportional to BD:DC
Now consider the two triangles PBD and PDC. They too share the same height if we consider segments BD and DC as their bases. Therefore,
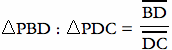
If we compare the two areas APB and APC, since
![]()
and we proved that the pairs of triangles ABD & ADC, and PBD & PDC are in the same ration of BD : DC, it follows that
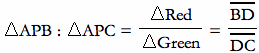
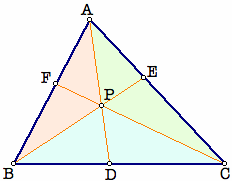
The ratio of the triangles red, green, and blue
Similarly we can show that
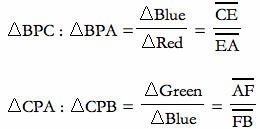
Now, if we multiply the three ratios we obtain
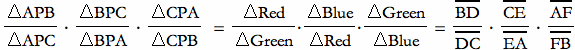
Because the three fractions involving the triangles (on the left and middle) cancel out to 1, we get
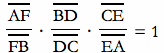
And the proof of Ceva's Theorem is almost completed. We have proved the first part of Ceva's theorem, but we also need to show that the opposite is also true. That is, if the multiplication of the three ratios is one, then the three lines AD, BE, and CE intersect at one point.
Let us assume that the three ratios multiply to 1, That is,
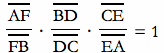
Let us say that the two lines BE and CF intersect at point Q inside the triangle. Then we can connect the vertex A to this intersection point Q as in the following diagram. We need to show that an extended segment from A though Q intersect the side BC at point D.
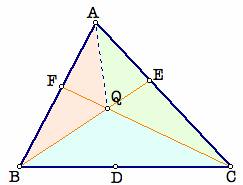
If the three ratios multiply to 1, then are A, Q, and D concurrent?
Then, from the first part of our proof, we know that
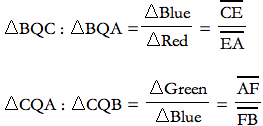
If we multiply these two ratios, then we get,

Initially, we assumed that the three ratios multiply to 1. Hence,
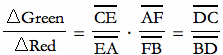
Let us extend the segment AQ until it meets the side BC and label the intersection point D'. The from our first part of the proof, we know that the ratios of area Green to Red will equal to the ratio D'C : BD'. However, from our assumptions and the equation right above us, the ratio of areas Green : Red must equal to DC : BD. Thus, D must coincide with D'. Therefore, the extended segment from vertex A to point Q intersects the opposite side at point D. We have proved that if the three ratios multiply to 1, then the three lines AD, BE, and CF are concurrent.
And the proof of Ceva's theorem is complete!
The three medians of the triangle intersect at one point. This can be proved quite easily using Ceva's Theorem. To see the proof, CLICK HERE.