

Valerie Russell
Final Project
Part 1:
I have chosen to continue my explorations of Parametric curves in Assignment 10 using Investigation 4.
The ranges of the x and y variables are often easily determined in parametric form. Let's take a look.
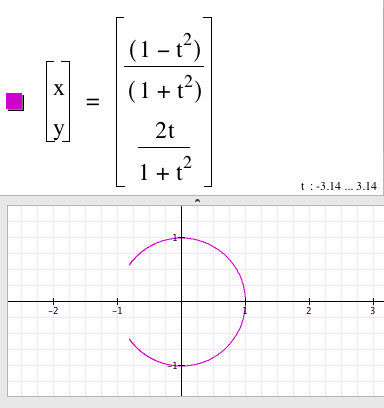 |
This parametric equation in the interval -3.14 < t < 3.14 appears to be an incomplete circle. |
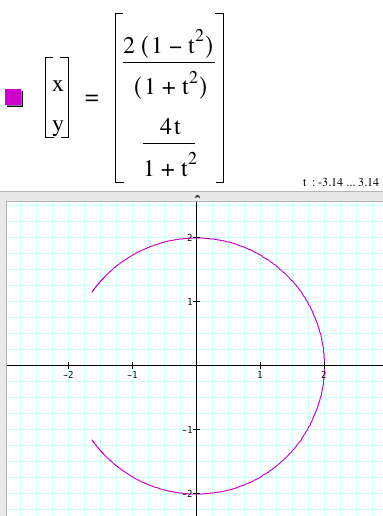 |
Let a = the coefficient of the x parameter. Let b = the coefficient of the y parameter.
The X Parameter In the previous graph, the a coefficient is 1. In this graph the a coefficient is 2. In both cases it appears that as the coefficient of the x parameter increases, the radius of the circle also increases by that amount. The Y Parameter In the previous graph, the b coefficient is 2. In this graph the b coefficient is 4. In both cases it appears that if this was a full circle, the length of the diameter would be the same as the b of the y parameter. |
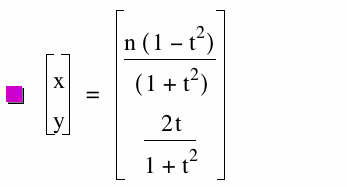 |
Notice what happens along the x axis. What once appeared to be an open circle now appears to be an open ellipse. As a increases the length of the horizontal axis increases, 0 < a < 10. The length of the semi-horizontal axis is a.
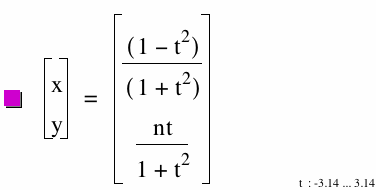 |
WOW! The open ellipse has changed direction. As 0 < b < 10 the major axis is vertical. The length of the vertical axis is b.
Other Changes
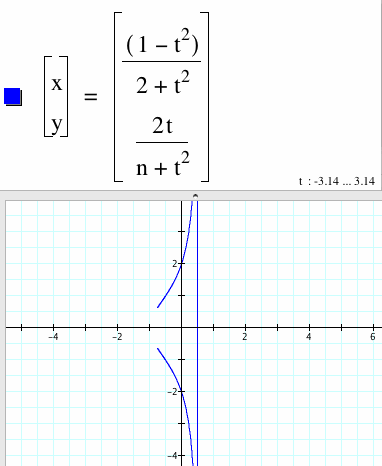 |
As the 1 in the denominator changed to 2 in the x parameter of the graph to the left, there is asymptotic behavior. The 2 produced an asymptote x= 1/2. Let's see what happens when this number is changed to 1/2. Just as I thought. The asymptote is the reciprocal of 1/2. It is 2. |
This graph allows you to see the changes in the vertical asymptotes as the denominator in the x parameter changes for any n. Can you guess what the 1/2 has become now? The vertical asymptote is at 5 so the 1/2 is now 1/5. As n increases in the y parameter, the graph expands vertically. As the n increases in the x parameter, an asymptote is created that is the reciprocal of n. |
Part 2
Bouncing Barney
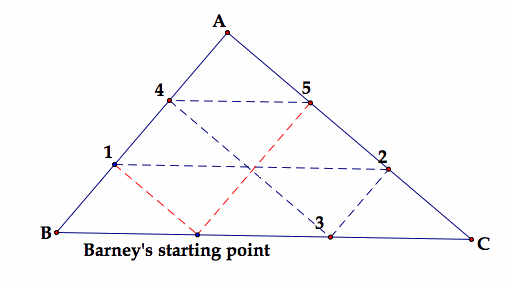 |
Barney is in the trianglular room shown to the left. The sides of the triangle represent walls. The dashed lines represent his path. The numbered points are the turns he makes when he hits a wall. Barney walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Barney's starting point is labeled along with his path. Barney hits a wall five times and walks along six different paths before returning to his starting point. Barney's path form triangles. Are they similar? |
A different starting point
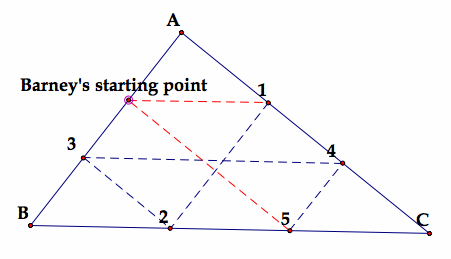 |
This time Barney starts at a point on wall AB. He begins walking towards AC in a path parallel to BC. When he reaches AC, he turns and walks parallel to AB. When he reaches BC, he turns and walks parallel to AC. When he reaches AB, he turns and walks parallel to BC and so on until he finally reaches his starting point again. Even though Barney chose a different staring point on the wall this time, he still hits a wall five times and walks along six diffferent paths before returning to his starting point. What would happen if Barney started at point 3 on wall AB instead of the original point. If you follow the path you will discover that it also leads back to its original starting point. We also see that Barney's path form triangles. We have parallel lines and transversals. Are these triangles similar? |
Barney's Path Forms Triangles
1. Using the midpoints of triangle ABC:
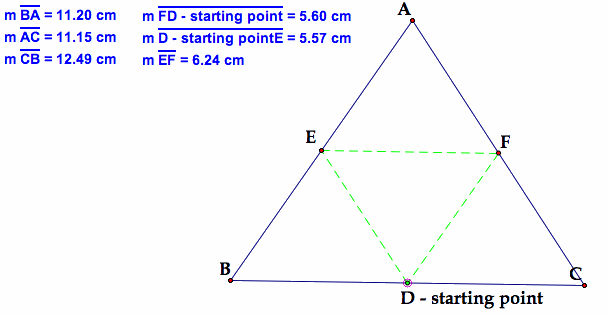 |
If Barney happens to start at the midpoint of BC and walks in a path parallel to AC, he will hit a point on wall AB that is also a midpoint. The same holds true for his path parallel to BC from the midpoint of AB to AC, then from his path parallel to AB from the midpoint of AC back to BC. There is a theorem that states, "If a line is parallel to one side of of a triangle and intersects the other two sides, then it forms two similar triangles." Therefore, triangle ADE, BDF, and CEF are all similar to triangle ABC. Hence, Barney will begin and end at the same point. His starting point is on the similar triangle. Another interesting theorem comes to mind in this problem. "If a midline of a triangle is parallel to the third side, then it is half as long as the third side."Therefore, DE=.5BC, EF = .5AB, and DF = .5AC. The ratio of triangle FED to triangle ABC is 1:2. |
We also know that if two figues are similar then their corresponding sides are proportional.


What if Barney begins his journey at the orthocenter?
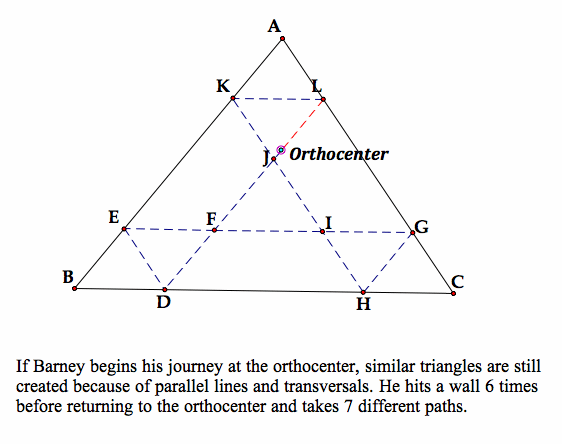
Let's look at Barney's journey from the centoid.
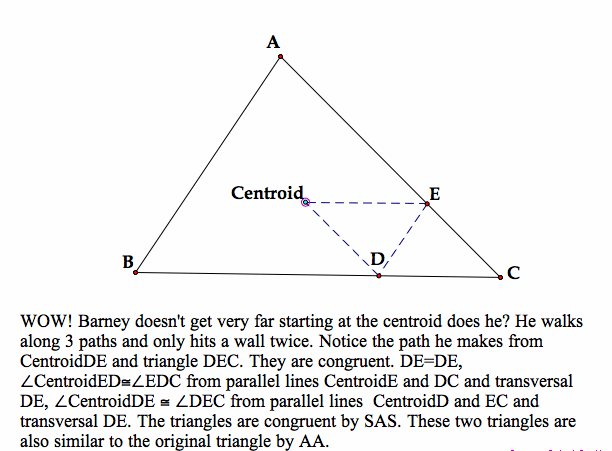
What if Barney wants to begin his journey outside the walls?
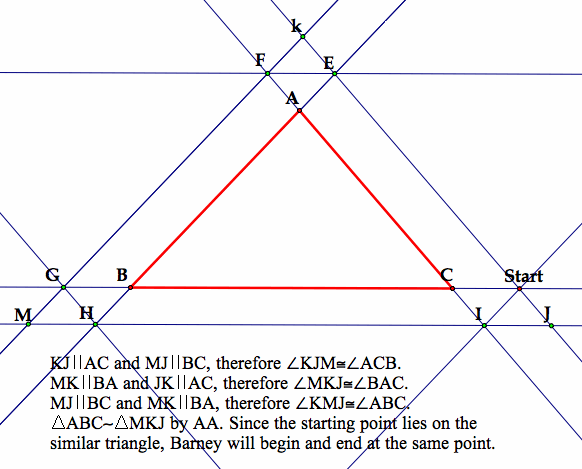
RETURN TO HOME PAGE