Valerie Russell

Assignment 1

Exploring Functions of the form y = a sin(bx + c)

Let's explore the graph of y = sin(x) and y = 2 sin(x) for x (the domain) in the interval [-π , π ] and determine the range of the functions.

Exploring a

If we multiply the y-coordinate of every point on the graph of

y = sin(x) by 2, we obtain all of the points on the graph of

y = 2 sin(x). As a increases, y = sin(x) is stretched and the range

increases. When a = 0 we get y = 0 which is a horzontal line or the

x-axis.

Now let's see what happens when a has a negative value:

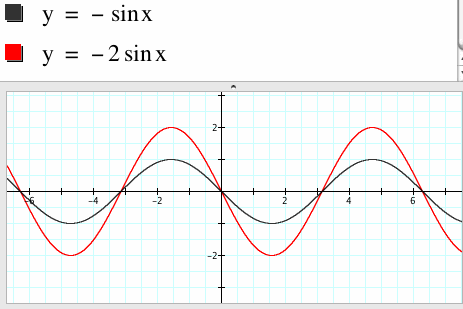Notice that the graph of y = -2sin(x) is stretched by a factor of 2. The negative sign flips the sine function upside down or refects the sine function across the x-axis.

Exploring b

Let's explore the graph of y = sin(x) and y = sin(3x).

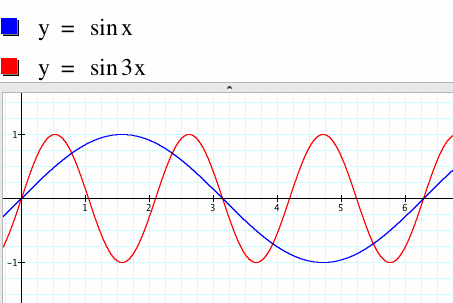We can see that y = sin(x) completes its cycle in the interval [0,3.14] whereas y = sin(3x) completes its cycle in the interval [0,2.09]. As b increases the period of the sine function decreases and vice-versa.

Let's see what happens if b is a multiple of π:

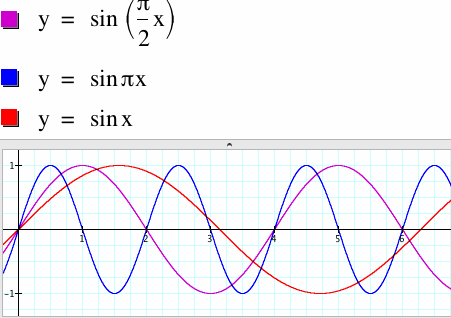Notice that one cycle of y = sin(π/2)x is completed in the interval [0,4] and y = sinπx is completed in the interval [0,2]. Anytime b is a multiple of π, the zeros of the sine function will be integers.

Hence, both a and b affect the shape of the curve. We saw that a affects the vertical stretch whereas b affects the period.

Exploring c

Now let's explore the graph of y=sinx and y=sin(x+π/6).

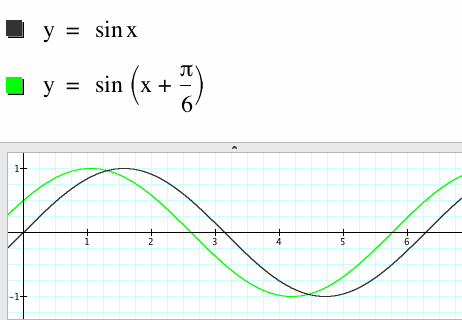	Notice that the graph of y = sin(x+π/6) is obtained by moving y = sinx a distance of π/6 (approximately .52) units to the left. The movement can be left or right and is derived by setting the expression in parenthesis equal to zero and solving for x. Ex: x + π/6 = 0 x = -π/6

y = sinx and y = 3sin(2x-π)

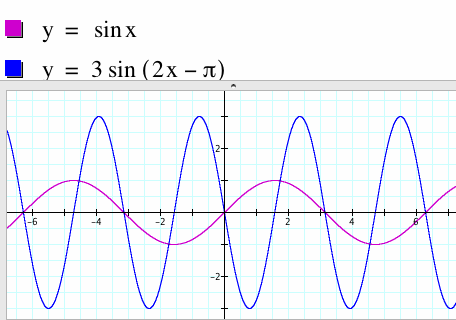If we factor out b and rewrite the function as y = 3sin[2(x-π/2)], we can see that a=3, b=2 and c= π/2. Notice a: The graph stretched vertically by a factor of 3. b: The period changed causing the cycle to shrink from 6.28 to 3.14 . c: The cycle shifted a distance of π/2 or 1.57 units to the right.

Extension

y = a sin(bx + c) + d

What happens if we add a constant to the sine function?

Notice that y=3sin(2x - π) + 1 moved up 1 unit whereas y=3sin(2x - π) - 2 shifted down 2 units. Adding a constant to the sine function shifts all the points vertically up or down.

Hence, while both a and b affect the shape of the curve, c and d affect the curves location.

Here's an exercise:

Suppose the volume of air V in cubic centimeters in the lungs of a certain distance runner is modeled by the equation V = 400sin(60πx) + 900, where x is time in minutes.

a) What are the maximum and minimum volume of air in the runners lungs?

b) How many breadths does the runner take per minute?

Solutions:

a) Remember that c and d affect the curves location whereas d moved the curve up 900 cubic cm. from a, 400 cubic cm. The maximun volume of air the lungs of a certain distance runner would be 900 + 400 or 1300cc. whereas the minimum volume would be 900 - 400 or 500 cc.

b) The x-axis is the time axis so the amount of time required for the volume of air in a runners lung to complete 1 cycle is 2π/b and the number of cycles per unit of time is the reciprocal b/2π. Therefore, 60π/2π = 30 breadths/min.

RETURN TO HOME PAGE