

Valerie Russell
Assignment 12
Buying a house with mortgage.
Most of us are aware that a big part of the "American Dream" is to own your own home. What we may not realize is that in addition to having a place to call your own, it also serves as a wise financial investment.
Buying a house with a long term loan called mortage, is the largest purchase of a lifetime for most people. The purchaser will normally be commited to 10, 15, 20, 25, or 30 years of mortgage pqyments. The two most popular types of loans today are the adjustable rate loan (variable rate loan) and the conventional loan You can calculate the principle and the interest for all the payments. athis is a tedious task. A list containing a payment number, payment on the interest, payment on the principal, and balance of the loan, can be prepared using a computer spreadsheet program. This list is called a loan amorization schedule. You must know the
in order to get the monthly payments.
Let's look at an example:
 |
Sally jacobs wishes to buy a house selling for $250,000. Her credit union requires her to make a 15% down payment. The current mortgage rate is 4.5%. A) Determine the amount of the required down payment. B) Determine a monthly mortage payment for a 10, 15, 20, 25, or 30 year loan with a 15% down payment. C) Make a loan amorization schedule for Sally. How many years will it take Sally to pay off her house? How much money will she pay in interest? |
A) The down payment is 15% of 250,000 or 0.15 x 250,000 = 37,500.
The mortgage on Sally's new home is the selling price minus the down payment $250,000 - 37,500 = 212,500.
B) To determine Sally's monthly mortgage payments of principal and interest, first divide the mortgage by 1000.
$212,500 / 1000 = $212.50
Lending institutions and lawyers use computer programs or calculators to determine monthy mortgage paymens, per thousands of dollars, for a specific number of years at a specific rate. They multiply the number of thousands of dollars by the number found on the chart. In Sally's case, if she wanted to payy off her mortgage in 10 years, the monthly mortgage payments would be:
$212.50 x 10.36 = $2,201.50.
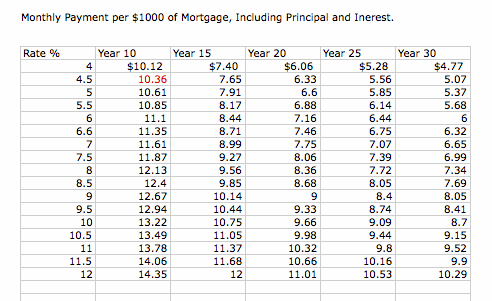
This table was taken from: Angel A. R., Abbot C. D., Runde D. D., A Survey of Mathematics with Applications, 7th edition, (p. 638).
The longer the term of the mortage, the more expensive the total cost of the house. To determine how much Sally will be able to afford, the lender takes 22% of Sally's income 100,000 x .22 = 22,000, then divides it by 12, 22,000/12 = $1,833.33. Sally can afford to pay $1,833.33 a month on her mortgage payments. As you can see, Sally will not be approved for a 10 year loan. She will have to look at a 15 year loan.
$212.50 x 7.65 = $1,625.63
As you can see, a 15 year loan will best fit Sally's budget.
Another way to is to use an amorization caculator using Excel.
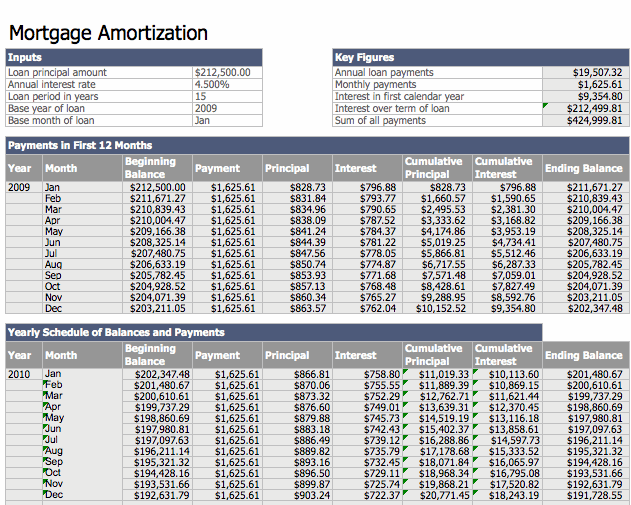
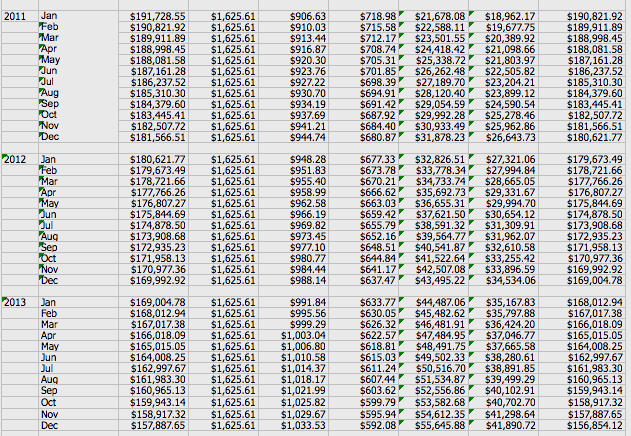
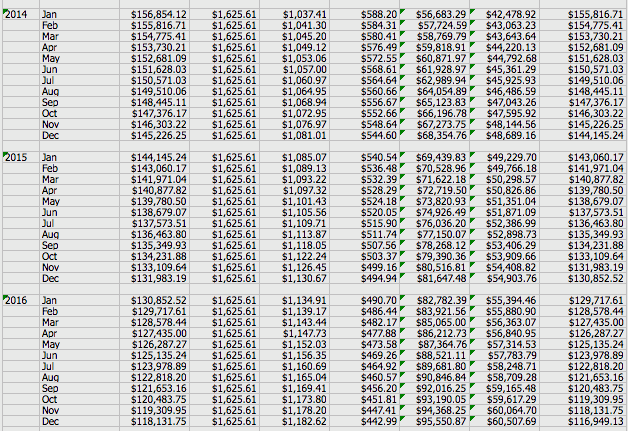

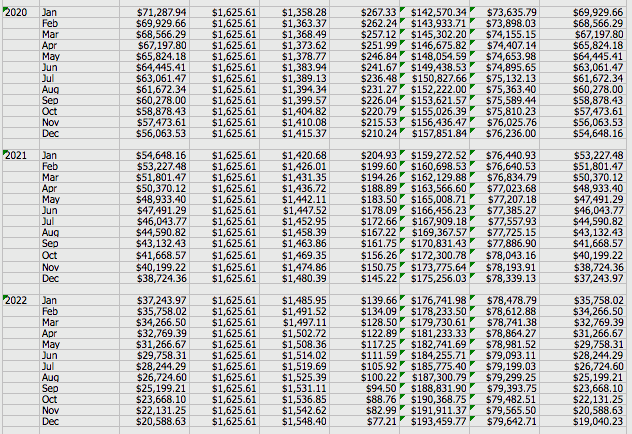
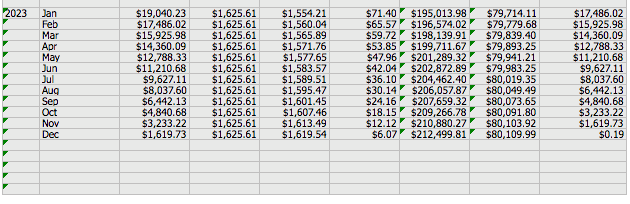
The lender was able to show Sally all of her interest payments for 15 years. Under Key Figures at the top of the chart, it shows Sally's total interest payments over a 15 year period to be $212,499.81. WOW!
RETURN TO HOME PAGE