Valerie Russell

Assignment 8

Altitudes and Orthocenters

Constructing Orthocenters:

The orthocenter is the point of concurrency of the three altitudes of a triangle. I constructed the orthocenter of triangle ABC and labeled this point H.

Point H allowed me to form other triangles, HAB, HBC, and HAC. I constructed the orthocenters of each of the new triangles formed from point H. Triangles HBC and

BHA haveothocenters outside of the triangle. I conclude that this happens whenever the triangles are obtuse. The orthocenter of triangle HAB is found on triangle ABC at

point C. The orthocenter of triangle HAC is found on triangle ABC at point B. It was interesting to find that the orthocenter of triangle HAB coincided with pont C and

the orthocenter of triangle HAC coincided with point B.

Constructing Circumcenters:

The pont of concurrency of the three perpendicular bisectors of the sides of a triangle is the circumcenter. I constructed the circumcenter of each of the four triangles,

ABC, HBC, HAB, and HAC. As each vertice of triangle ABC is moved to the orthocenter H, the three triangles become one triangle. I also found that the circumcenter

is equally distant from all three vertices of the triangle. By using the circumcenter and a vertice of each triangle I was able to construct the circumcircle of each of the

four triangles. The following is a model of the construction.

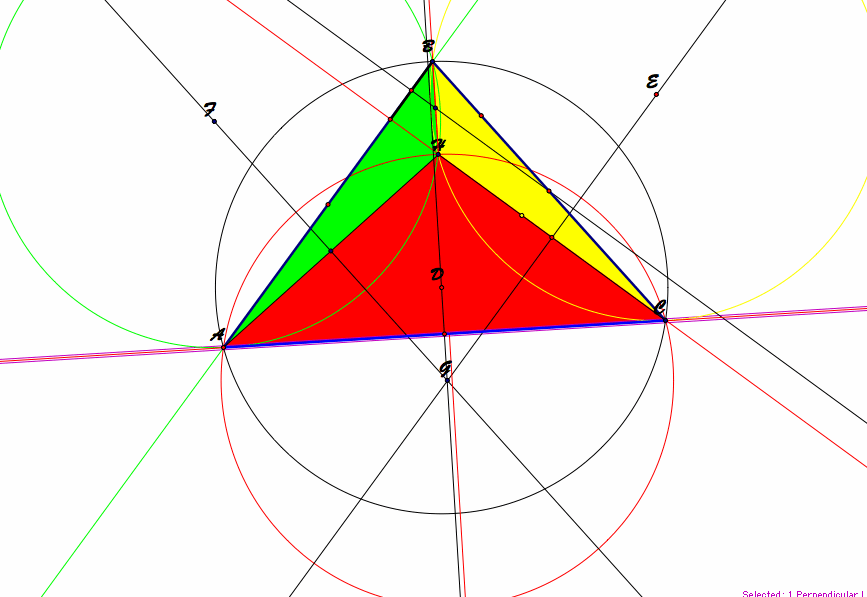
All of the circumcircles appear to have the same areas.

Click here to see Animation.

The Nine Point Circle

In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant points, six lying on the triangle itself (unless the triangle is obtuse). They include:

* The midpoint of each side of the triangle (H4, H6, H9)
* The foot of each altitude (H1, H3, H7)
* The midpoint of the segment of each altitude from its vertex to the orthocenter (where the three altitudes meet). (H2, H5, H8).

Here is an example:

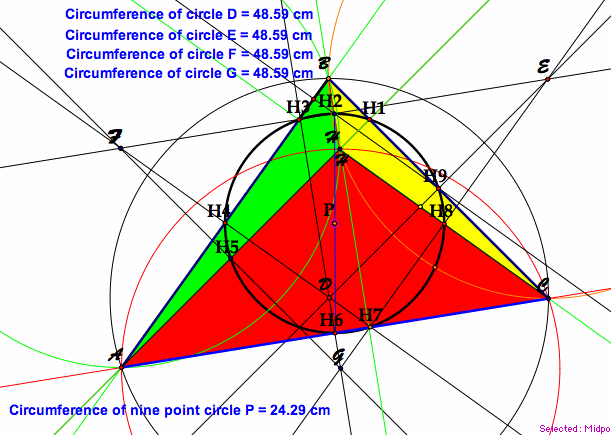This diagram is an extension of the first and shows the significant points of Circle P as being a Nine-Point Circle. You can follow the points H1, H2, H3, H4, H5, H6, H7, H8, and H9. Notice that all of the circumferences of the circumcircles for the 4 triangles are the same. We can conclude that the areas for these triangles will also be the same. The area of the nine point circle appears to be half of the area of the circumcircle.

The following proof of the Nine Point Circle was adapted from a proof on the website of the Computer Science and Mathematics Department, Arakansas State University http://www.csm.astate.edu

The theorem:

Given triangle ABC. Let point H4 be the midpoint of side AB, point H6 be the midpoint of side AC, and point H9 be the midpoint of side BC (Note triangle H4H6H9 is the medial triangle).

Let point H3 be the foot of the altitude from point C to side AB, point H7 be the foot of the altitude from point B to side AC, and point H1 be the foot of the altitude from point A to side BC (Note triangle H3H7H1 is the orthic triangle).

And if point H is the orthocenter of triangle ABC, let point H2 be the midpoint of HB, point H5 be the midpoint of HA, and point H8 be the midpoint of HC (Note triangle H2H5H8 is the orthocenter mid-segment triangle).

Prove points H4, H6, H9, H3, H7, H1, H2, H5, and H8 lie on a common circle (called the nine-point circle).

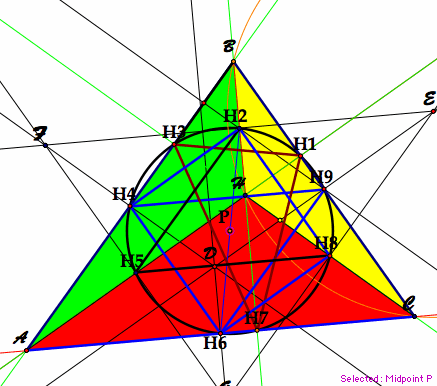
The proof:

In triangle ABC, since H4 and H6 are midpoints of sides AB and AC (by construction), then segment H4H6 is parallel to side BC.

In triangle BCH, since H2 and H8 are midpoints of sides BH and HC (by construction), then segment H2H8 is parallel to side BC.

Since segment H4H6 is parallel to side BC, and segment H2H8 is parallel to side BC, then segments H4H6 and H2H8 are parallel to each other.

In triangle BAH, since H2 and H4 are midpoints of sides BH and BA (by construction), then segment H2H4 is parallel to side HA.

In triangle CAH, since H6 and H8 are midpoints of sides AC and HC (by construction), then segment H6H8 is parallel to side HA.

Since segment H2H4 is parallel to side HA, and segment H6H8 is parallel to side HA, then segments H2H4 and H6H8 are parallel to each other.

Since segment H2H4 is parallel to segment HA, and segment HA lies on segment AH1, then segment H2H4 is parallel to segment AH1.

Since segment AH1 is perpendicular to side BC by construction (AH1 is the altitude from point A to side BC), and side BC is parallel to segment H4H6, then segment AH1 is perpendicular to segment H4H6.

Since segment H2H4 is parallel to segment AH1, and segment AH1 is perpendicular to segment H4H6, then segment H2H4 is perpendicular to segment H4H6.

Thus, we have that quadrilateral H4H6H8H2 is a rectangle. Since the opposite angles of this quadrilateral are supplementary, it follows that the quadrilateral can be inscribed in a circle.

Similarly, quadrilateral H4H5H8H9 is a rectangle, and it can be inscribed in a circle.

Therefore, points H4, H5, H6, H8, H9, and H2 are on a common circle, with one diameter of the circle being segment H4H8, since this segment is a diagonal of both rectangles. The center of this circle, then, is the midpoint of segment H4H8. Let this center be point O.

Now, since segment AH1 is an altitude, angle H5H1H9 is a right angle. But segment H5H9 is also a diameter of our circle (it is a diagonal of rectangle H4H5H8H9), so it follows that point H1 must lie on this circle.

Similarly, points H3 and H7 are on the circle.

Therefore, all nine points H4, H6, H9, H3, H7, H1, H2, H5, and H8 lie on the same circle, called the nine-point circle.

BACK TO HOME PAGE