Valerie Russell

Assignment 9

The Pedal Triangle

What is a Pedal Triangle?

Given a triangle and any point in the plane, the triangle formed by the perpendiculars to the sides of the triangle is called the Pedal triangle for the pedal point.

(Also known as Nested Miquel triangles)
As mentioned before, the triangle whose vertices are the feet of the perpendiculars from a point P inside a triangle ABC to each of its sides AB, BC and AC, is called a pedal triangle.

The pedal triangle has many interesting properties, but the following one is particularly interesting:

Neuberg's theorem: If a sequence of nested pedal triangles from the same point P is constructed, then the third pedal triangle is similar to
the original triangle ABC.

In other words, the pedal triangle of a point with respect to the pedal triangle with respect to the pedal triangle with respect to the triangle is similar to the original triangle? Let's take a look.

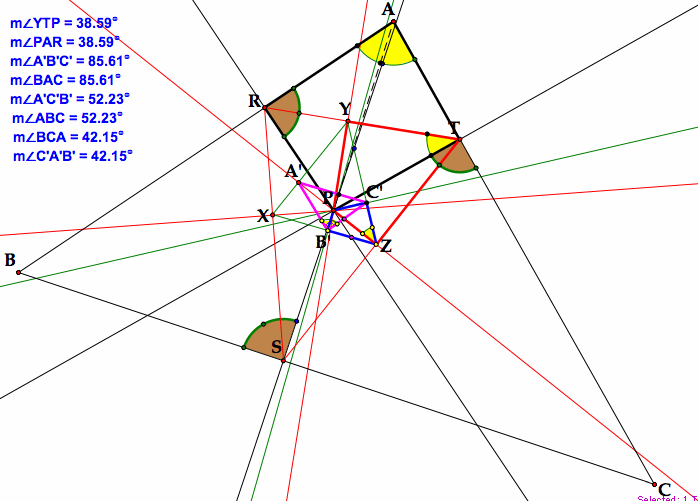
Now let's prove that the pedal triangle A'B'C' of the pedal triangle XYZ of the pedal triangle RST of a point P is similar to the original triangle CAB.

Proof: A proof immediately becomes apparent when we construct the perpendicular segment PA.

<PSB = <PTC = <PRA

From the construction of the perpendicular lines to the sides, we have that
quadrilaterals ARPT, YPZT and C'PB'Z are all cyclic.

Therefore, <PAR = <PTR = <PZY =<PB'C'.

Similarly, we can show that <PAT = <PB'A'.

Thus, <C'B'A' = <BAC. In the same way, the equality of
corresponding angles at B and C' or C and A' can be established.

Reflection:
Since the Miquel triangles can be constructed arbitrarily at each stage, I
realized that this implied that they are all similar at each stage; indeed
they all had to be similar to the respective pedal triangles at each stage

Published in Math Gazette, Nov 2002, 86(507), pp. 390-395. Copyright Mathematical Association.

RETURN TO HOME PAGE