Assignment 10: Parametric Equations

Ebru Ersari

Consider the parametric equations for

Graph these for a / b = 1/2, 1/4, 2/3, 12/13, etc.
Describe fully. You may have to increase the range of t for the larger fractions. This class of parametric curves are called the Lissajous curves. Compare with
x = sin ((a)t)
y = sin ((b)t)

Here are the graps of the parametric equations
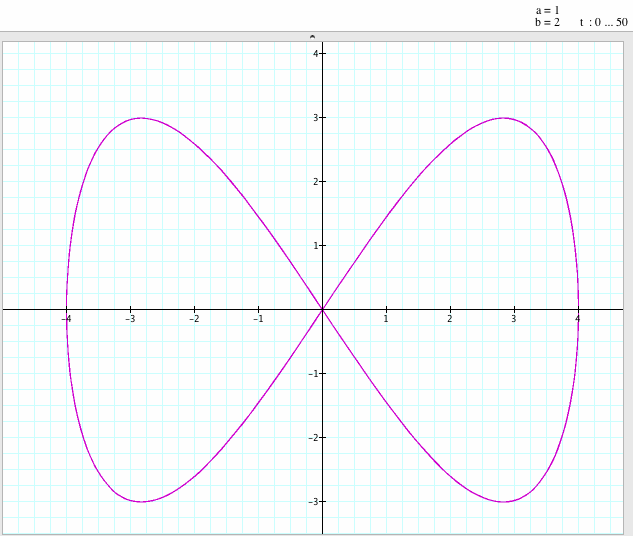
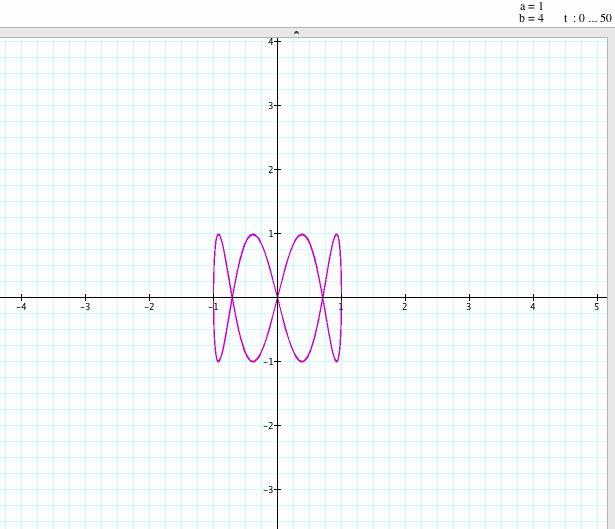
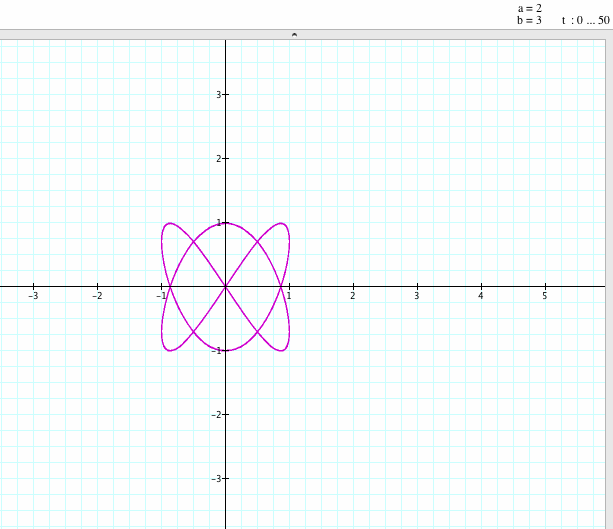
x = 4 sin ((a/b)t)
y = 3 sin(t)
and
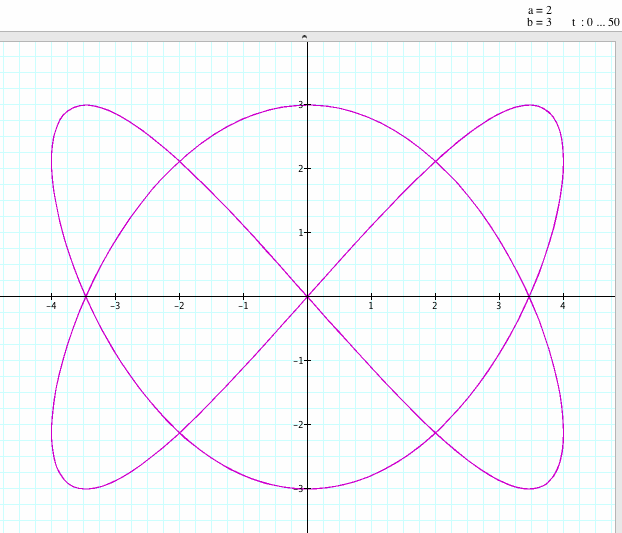
x = sin ((a)t)
y = sin ((b)t)
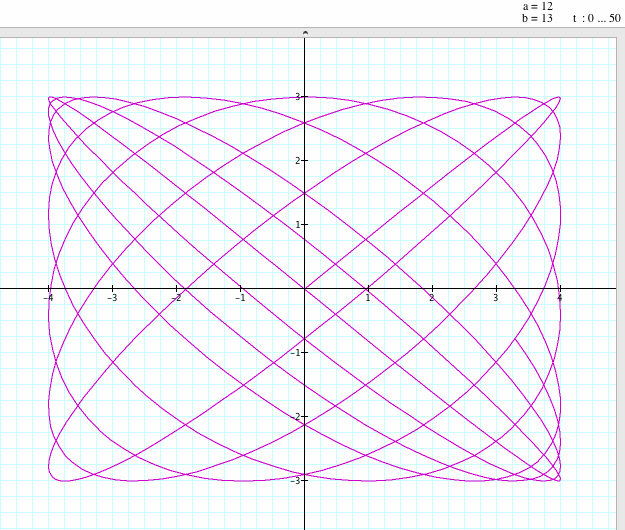
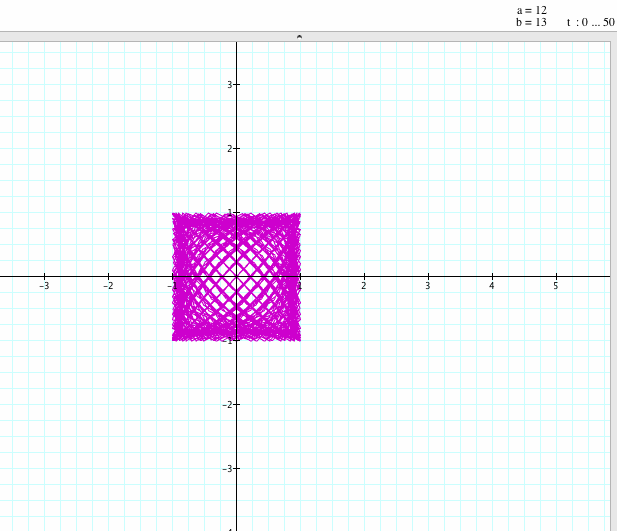
for 0 ≤ t ≤ 50 and a / b = 1/2, 1/4, 2/3, 12/13.

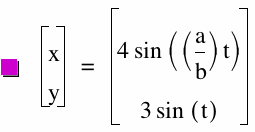
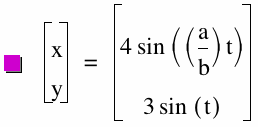
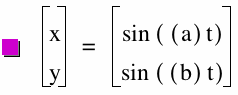
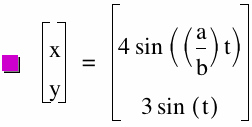
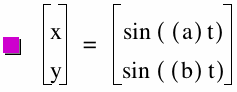
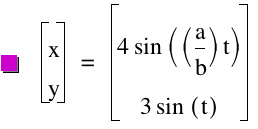
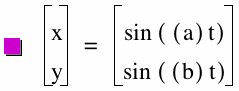
For trigonometric functions, the distance from the midpoint to the highest or lowest point of the function gives us the amplitude (A). For x = A(sin (B)t )function, the amplitude of the function is A.
x parameters of the graphs are x = 4 sin ((a/b)t) and x = sin ((a)t). When we compare these two functions, the amplitude of the function x= 4 sin ((a/b)t) is always 4 regardless of a/b values. Because 4 is a constant number and is independent of a / b ratio. For the same reason, the amplitude of the function x = sin ((a)t) is always 1.
y parameters of the graphs are y = 3 sin (t) and y = sin ((b)t). The amplitude of the function y = 3 sin (t) is 3 and the amplitude of the function y = sin ((b)t) is 1.

If a / b = 1/2, both graphs have similar shapes; we get a closed graph: two loops and one knot at the origin. However, the first graph, Lissajous curves, is from -4 to +4 and the second graph is from -1 to +1. The shapes are similar but the intervals are different.
If a / b = 1/4, 2/3, or 12 / 13: x = 4 sin ((a/b)t), y = 3 sin(t) and x = sin ((a)t), y = sin ((b)t) have similar shapes; we get a closed graph, again. Lissajous curves is from -4 to +4 and the second graph is from -1 to +1. The shapes are similar but the intervals are different as the previous comparison.

Return