

Assignment 12:The Spreadsheet in Mathematics Explorations
Ebru Ersari
Generate a Fibonnaci sequence in the first column using f(0) = 1, f(1) = 1,
f(n) = f(n-1) + f(n-2).
a. Construct the ratio of each pair of adjacent terms in the Fibonnaci sequence. What happens as n increases? What about the ratio of every second term? etc.
b. Explore sequences where f(0) and f(1) are some arbitrary integers other than 1. If f(0)=1 and f(1)= 3, then your sequence is a Lucas Sequence. All such sequences, however, have the same limit of the ratio of successive terms.
Here are the fist 30 Fibonacci numbers listed below. The Fibonacci sequence start with f(0) = 1, f(1) = 1 and continues with the rule f(n) = f(n-1) + f(n-2).
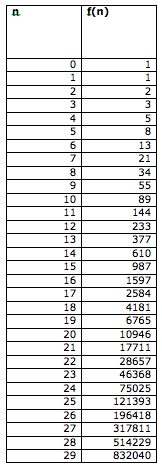
There are some patterns that we between the terms. What are these patterns between the terms?
First, let us look at the pattern between the adjacent terms. For the pattern, I look at the ratio of adjacent terms. Here is the table that shows the ratio of adjacent terms.
a(n)= f(n+1) / f(n).
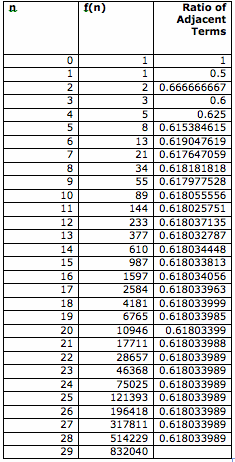
When n increases, the ratio of adjacent terms becomes a particular value. This value is close to 0.61803399.
What about the ratio of every second term? Does it also approach to a particular number, when n increases? Here is the table of the ratio of every second term.
b(n) = f(n+2) / f(n).
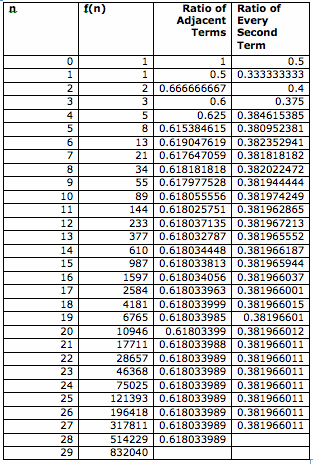
As n increases, the ratio of every second term becomes a particular value. This particular value is close to 0.38196601.
Then, I explored sequences for some arbitrary integers. Next two tables shows the ratio of adjacent terms and ratio of every second term for
f(0) = 1 and f(1) = 3 (this sequence is called Lucas Sequence)
and
for f(0) = 1 and f(1) = 5.
Here are the tables of the sequences.
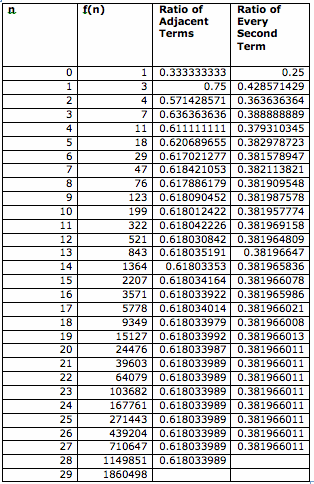
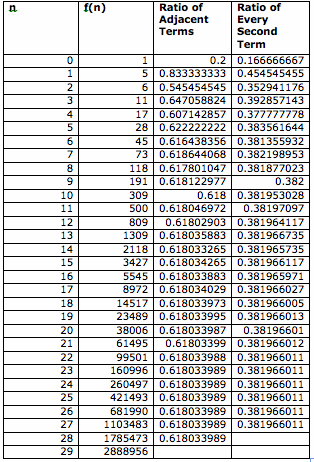
For the Lucas Sequence, when n increases, the ratio of adjacent terms approaches 0.61803399. We get this number for the Fibonacci Sequence, as well. Similar to Fibonacci Sequence, when we increase n, the ratio of the every second term approaches 0.38196601.
For f(0) = 1 and f(1) = 5: When we increase n, we get the same specific numbers. The ratio of adjacent terms approaches 0.61803399 and the ratio of every second term approaches 0.38196601.
When start with 1, we approach the same ratio for three sequences above. What about when we change the starting number? What if we start with f(0) = 2 and f(1) = 7 and have the same rule f(n) = f(n-1) + f(n-2)? Here is the table for the sequence.
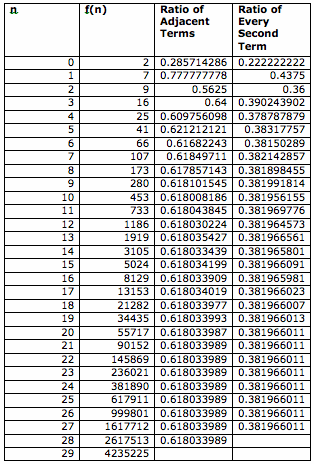
Even the sequence start with 2 rather than 1, we still get the same specific numbers for the ratios. The ratio of adjacent terms approaches 0.61803399 and the ratio of every second term approaches 0.38196601.
I investigate further for the ratio of every third term, fourth term, fifth term, sixth term etc. When we increase n, does it approach any specific number for these ratios? When we increase n:
For the third ratio of every third term, it approaches to 0.23606798.
For the fifth ratio of every fourth term, it approaches to 0.14589803.
For the fifth ratio of every fourth term, it approaches to 0.09016994.
For the sixth ratio of every fifth term, it approaches to 0.05572809.
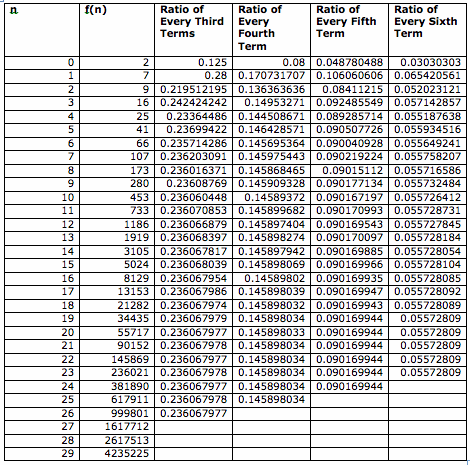
We can conclude that;