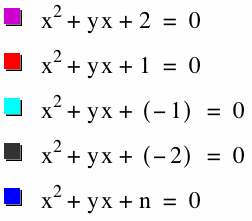Assignment 3: Graphs in the xb plane
Ebru Ersari
Consider again the equation x² + bx + 1 = 0. Graph this relation in the xb plane.
When I graph the equation, x²+yx+1=0, I draw it in the xy plane. When we want to graph x²+bx+1=0 in the xb plane,we name the y plane as the b plane. b values will be to the vertical axis (b axis).
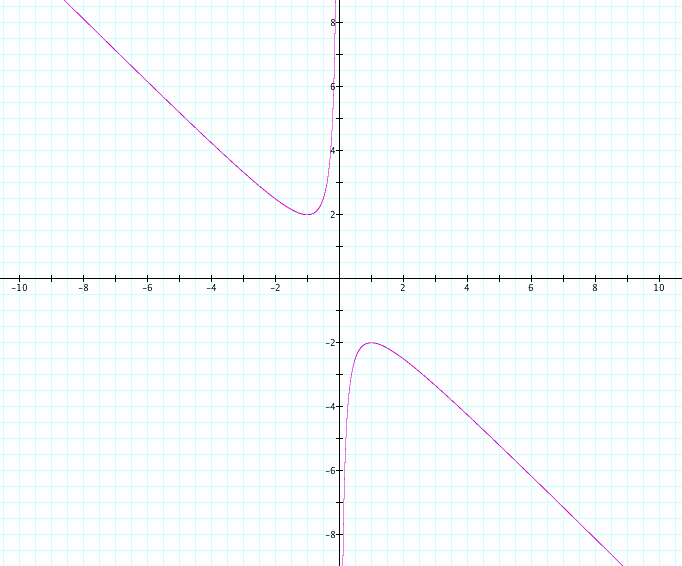
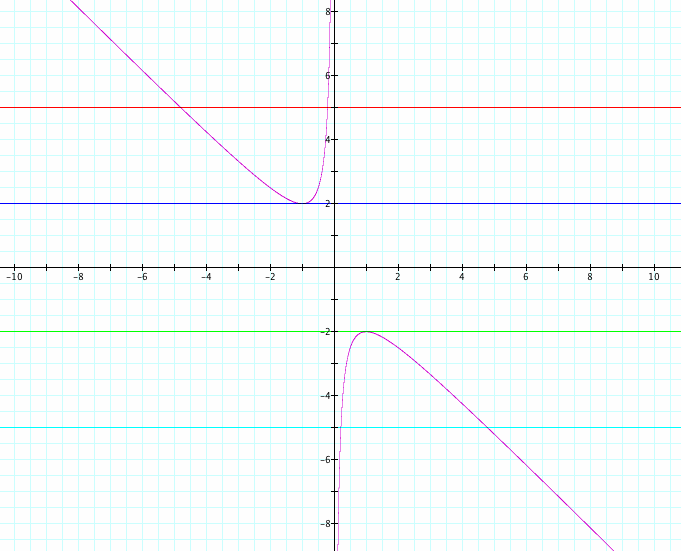
Here is the graph for the equation x²+bx+1=0.
Now, let’s investigate what happens for various b values.
I drew b = 5, b = 2, b = -2, b = -5 lines and found the intersection points with x² + bx + 1 = 0.
When b = 2 or b = -2, there the graphs intersect only in one point, so there is one real root for each. When b=2 there is one positive real root, when b = -2 there is one negative real root for x² + bx + 1 = 0.
When b > 2 and b < -2, the graphs intersect in two points and there are two real roots for each. When b > 2 there are two negative real roots, when b < -2 there are two positive real roots.
When -2 < b < 2, there are no intersection points. The equation x² + bx + 1 = 0 does not have any roots for -2 < b < 2.
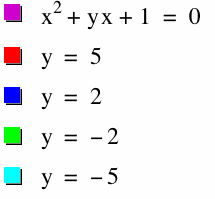
Here is another way of showing the number of roots.
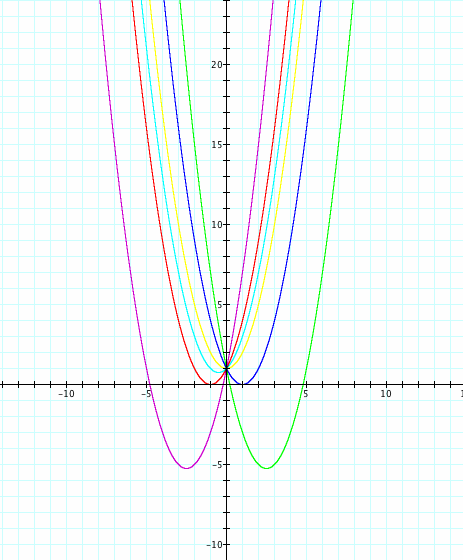
We know that for the number of real roots, we need to look at the number of points on the x axis. When we look at the graph;
x² + 5x + 1 = 0 and x² + (-5)x + 1 = 0 intersect the x axis in two points.
x² + 2x + 1 = 0 and x² + (-2)x + 1 = 0 intersect the x axis in one point.
x² + x + 1 = 0 and x² + 1 = 0 do not intersect the x axis.
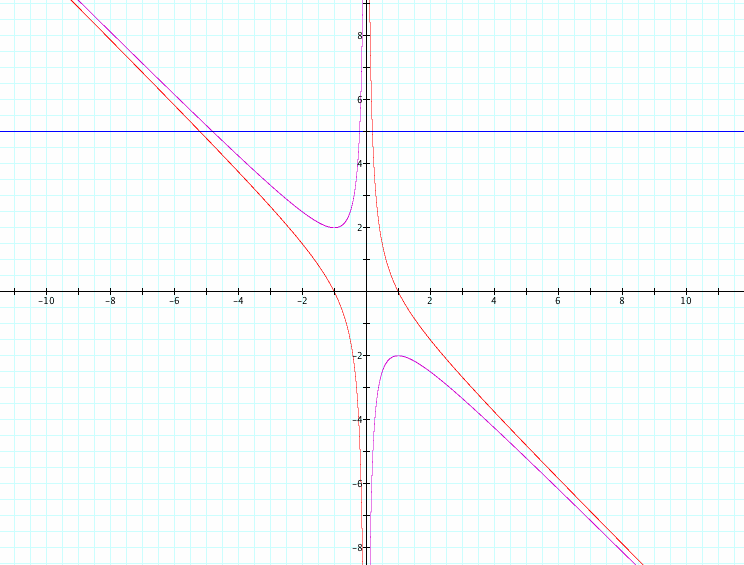
What if c = -1 rather than +1? Here are the graphs of x² + bx + 1 = 0, y = 5, and x² + bx + (-1) = 0
As we know, for the quadratic equation ax² + bx + c = 0,
The roots are
Considering the equation x² + bx + (-1) = 0, our a value is 1.
If 
> 0, there are two real roots.
If < 0, there is not any real roots.
If = 0, there is one real root.
Since = b² - 4ac and a = 1 in the equation x² + bx + c = 0,
= b²-4c and b²
0. Thus,
If c > 0: there will be two, one or no roots.
If c < 0: there will be always two roots (Always one of them is positive and the other one is negative).
If c = 0: there will be always two roots.
The other roots are:
x² + bx = 0
x(x+b) = 0
x = 0 or x = -b
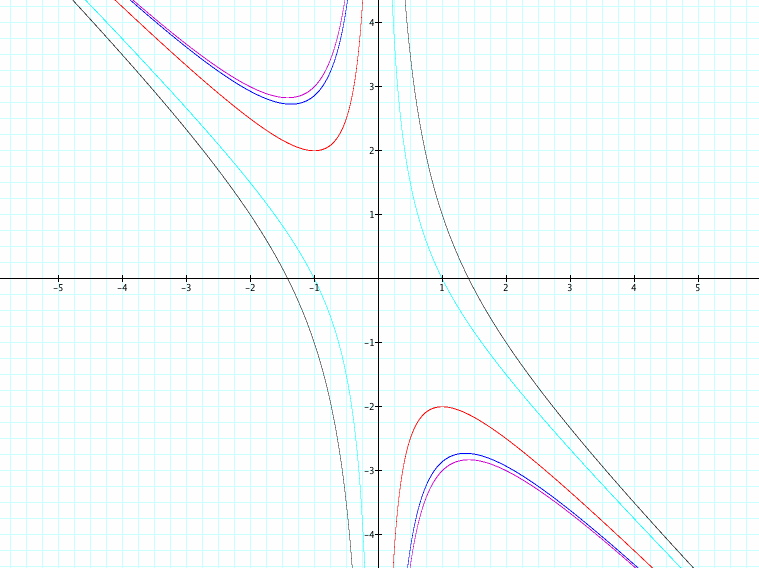
Here are some graphs for various c values.
