

Assignment 7: Tangent Circles
Ebru Ersari
Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.
We’ll look at 3 possibilities for the intersection of two circles in this problem:
First Case: One circle is inside another.
Second Case: Two circles intersect each other.
Third Case: Two circles are discoint.
First Case: Two circles intersect each other.
I constructed a circle which is tangent to two circles. For that construction, I took the blue circle with center O and passing through A, as the main circle ad I constructed a tangent circle to that circle. For constructing the tangent circle, I drew the green circle with center B and passing through C. Next, I took a point, point F, on the blue circle. I constructed the line passing through F and O. Then, I constructed the purple circle, the circle with center F, as the same radius with green circle. The center of the purple circle is on the line passing through F and O. I took point E, which is both on the line and purple circle. Then, I drew the segment passing through B and E. Later, I took the midpoint of the segment BE and named it point D. Next, I drew a perpendicular line to segment BE at point D. I took the intersection point of line k and line l. I named the intersection point as point G. For the final step, I constructed the brown circle with center G and passing through F. The brown circle is tangent to both blue circle and green circle.
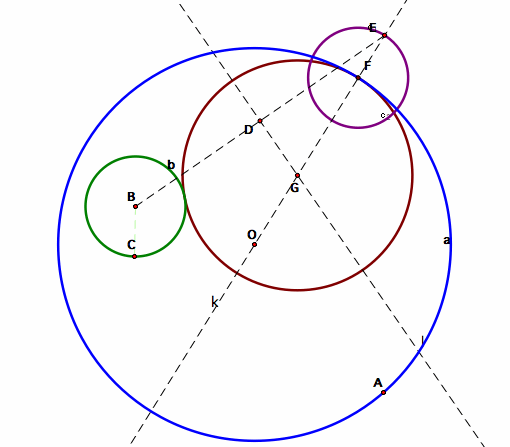
When we animate point F, the trace of point G will give us the ellipse.
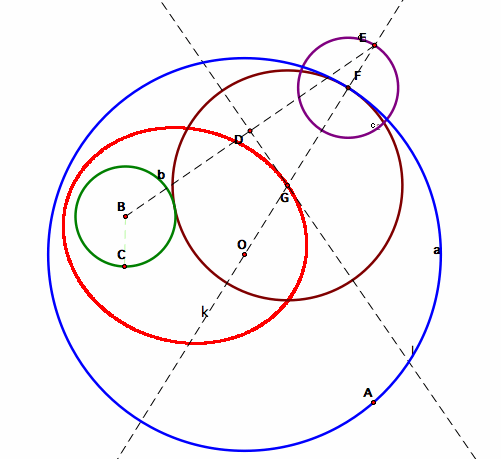
Here is the trace of line l when we animate point F. The untraced part is an ellipse.
Second Case: Two circles intersect each other.
When we repeat what we did in the previous case, we’ll get the brown circle above.
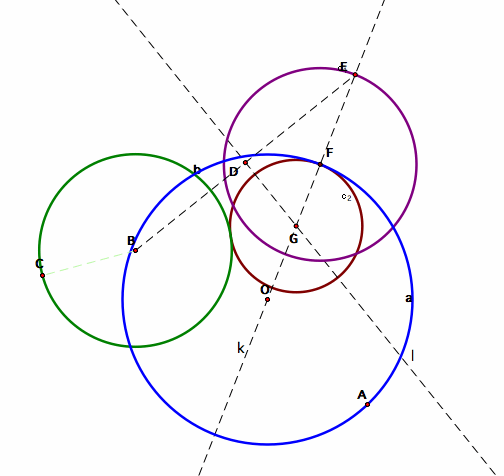
Similarly, when we animate point F and trace point G, this gives us an ellipse.
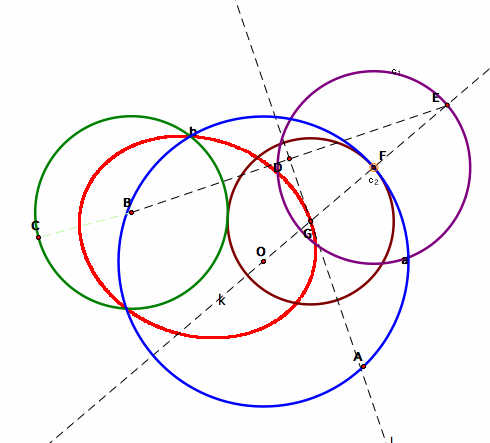
Here is the trace of line l by animating point F. The untraced part gives us an ellipse.

Third Case: Two circles are discoint.
Again, when we repeat the same process as we did for the first and second case, we’ll get the brown circle which is tangent to the both green and blue circles.
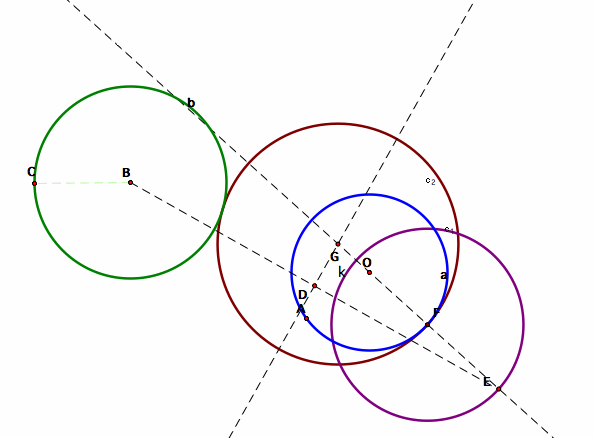
When we animate point F and trace point G, we get a hyperbola.
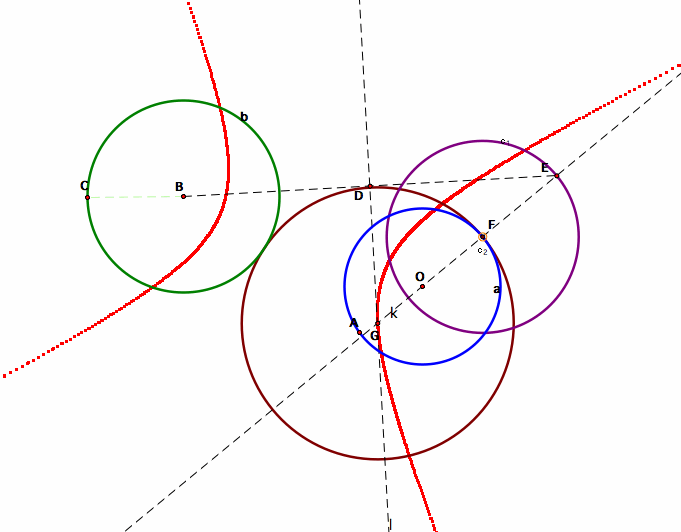
When we trace the perpendicular line by animating point F, the untraced part gives us a hyperbola.
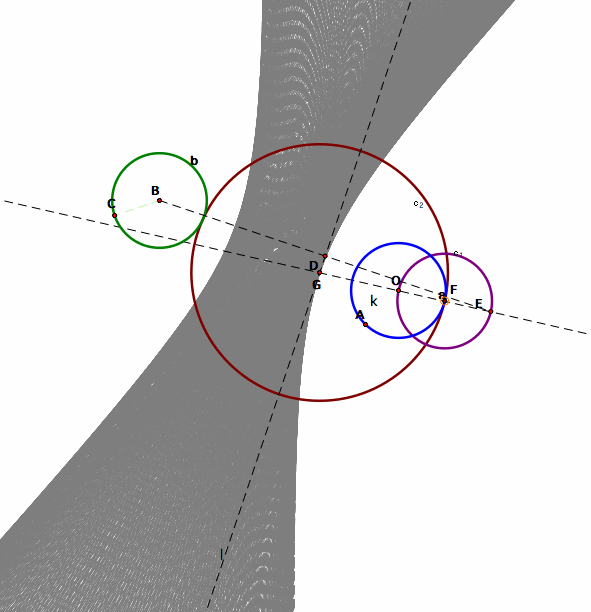
Conclusion:
When one circle is inside another or two circles intersect each other: The center of the tangent circle’s trace by animating point of tangency gives us an ellipse.
When two circles are discoint: The center of the tangent circle’s trace by animating point of tangency gives us a hyperbola.