

Assignment 8:Altitudes and Orthocenters
Ebru Ersari
1. Construct any triangle ABC.
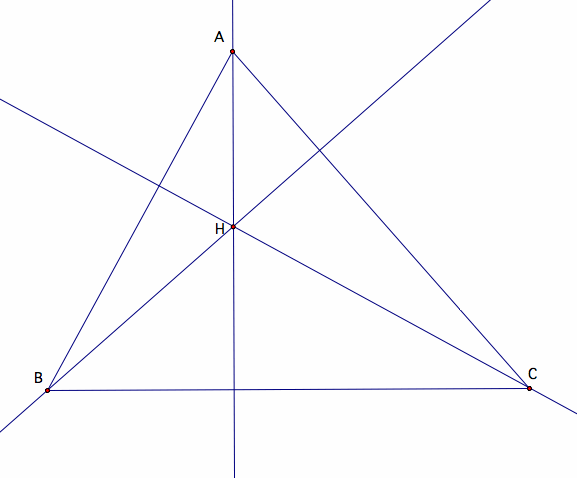
2. Construct the Orthocenter H of triangle ABC.

In triangle BHC,
The altitude from point B to segment CH is on the same line with the segment AB.
The altitude from point C to segment BH is on the same line with the segment AC.
The altitude from point H to segment BC is on the same line with the segment AH.
The intersection of three altitudes or their extensions intersect in point A.
3. Construct the Orthocenter of triangle HBC.

In triangle ABH,
The altitude from point H to segment AB is on the same line with the segment HC.
The altitude from point A to segment BH is on the same line with the segment AC.
The altitude from point B to segment AH is on the same line with the segment BC.
The intersection of three altitudes or their extensions intersect in point C.
4. Construct the Orthocenter of triangle HAB.
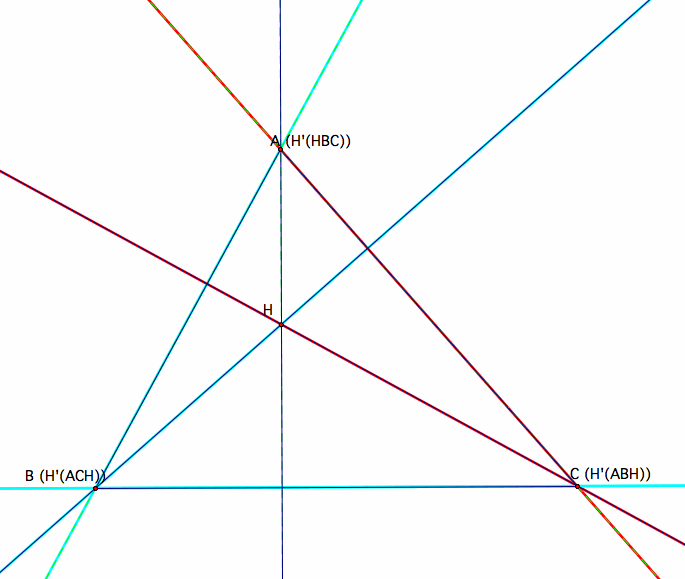
In triangle ACH,
The altitude from point A to segment CH is on the same line with the segment AB.
The altitude from point C to segment AH is on the same line with the segment BC.
The altitude from point H to segment AC is on the same line with the segment BH.
The intersection of three altitudes or their extensions intersect in point B.
5. Construct the Orthocenter of triangle HAC.

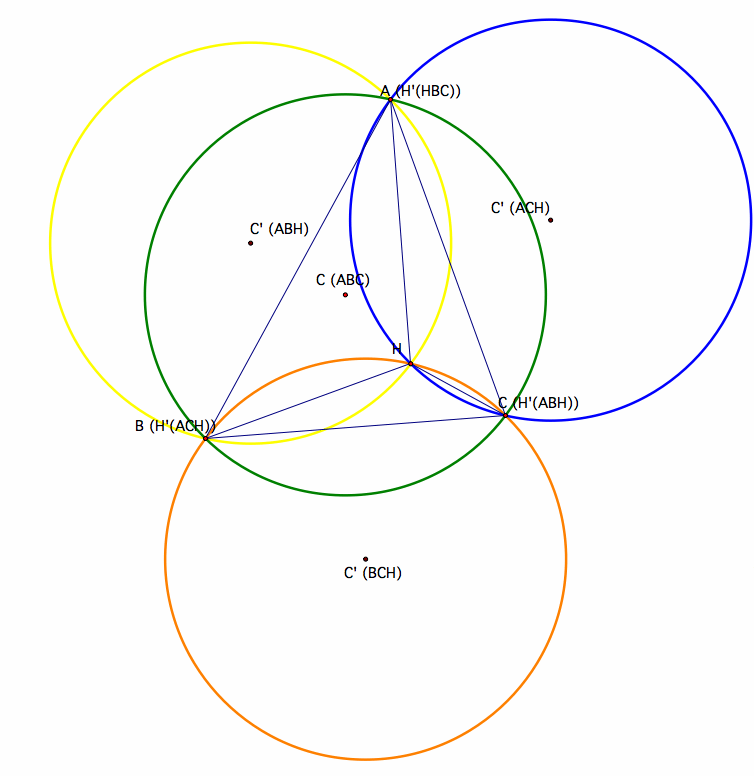
Now, let us find the circumceter of triangles ABC, BCH, ABH and ACH.
C (ABC) is the circumcenter of triangle ABC.
C' (BCH) is the circumcenter of triangle BCH.
C' (ABH) is the circumcenter of triangle ABH.
C' (ACH) is the circumcenter of triangle ACH.
6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.
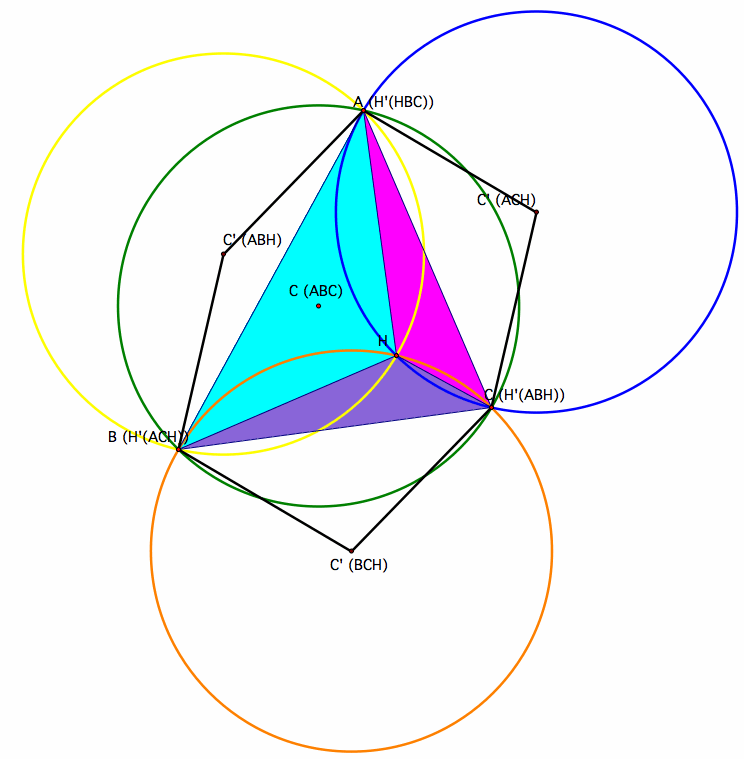
Green circle is the circumcircle of triangle ABC.
Yellow circle is the circumcircle of triangle ABH.
Blue circle is the circumcirle of triangle ACH.
Orange circle is the circumcircle of triangle BCH.