

Final Assignment (PART2): Extra Write-Up
Ebru Ersari
Graph
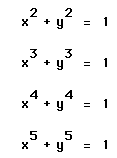
What do you expext for the graph of ![]() or
or ![]()
Let us start with graphing the first four functions above.
![]()
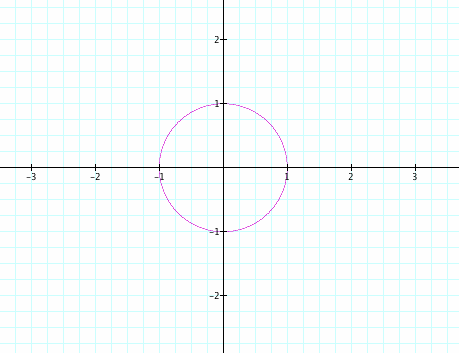
When we graph x^2 + y^2 = 1, we get a circle with radius 1. The center of the circle is the origin.
![]()
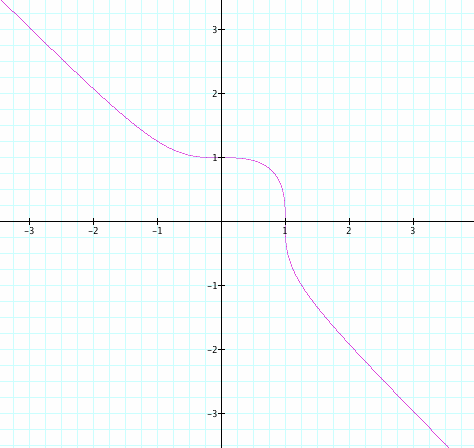
When we graph x^3 + y^3 = 1, we get a shape similar to y = -x function except between -1 and +1. In this interval, the graph looks like one fourth of the circle in the first quadrant. The line part is in the second and fourth qudrant and the circle part is in the third quadrant. (They are not exactly line or part of the circle but they look similar to a line and one fourth of the circle in the middle).
![]()
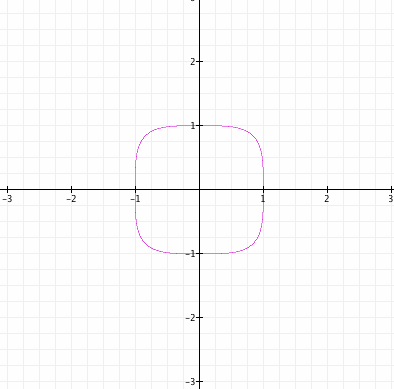
When we graph x^4 + y^4 = 1, we get similar shape to a square but the edges look like a circle.
![]()
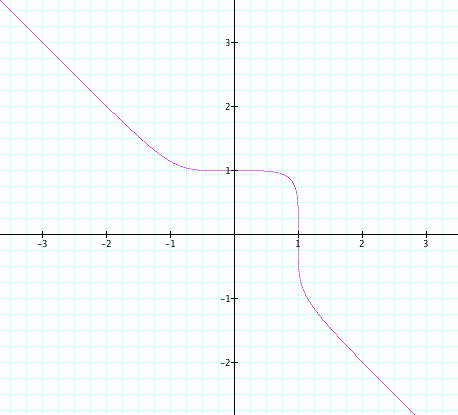
The graph of x^5 + y^5 = 1 is similar to x^3 + y^3 = 1. However, the graph between -1 and +1 is more likely x^4 + y^4 = 1in the first quadrant.
My expectations for x^24 + y^24 = 1: Since 24 is an even number, I looked at the graphs of the exponents with even numbers (x^2 + y^2 = 1 and x^4 + y^4 = 1). Both have similar shapaes but when the exponent's value increases, the shape looks more likely a square rather than a circle. Thus, I thought x^24 + y^24 = 1 might be very similar to a square.
My expectations for x^25 + y^25 = 1: Since 25 is an odd number, I looked at the graphs of the exponents with odd numbers (x^3 + y^3 = 1 and x^5 + y^5 = 1). Both have similar shapes but when the exponent's value increases, the shape between -1 and +1 looks more likely a square rather than a circle. Thus, I thought x^25 + y^25 = 1 might look like a line except the interval -1 and +1 and in this interval it might be more likely a square rather than a circle.
Here are the graphs of x^24 + y^24 = 1 and x^25 + y^25 = 1.
![]()
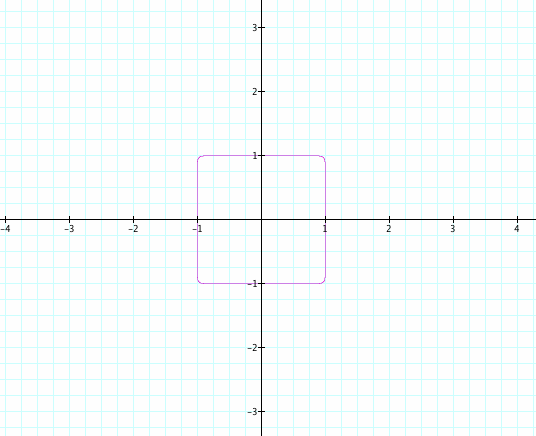
As I expected, the graph looks like a square. Compare to x^2 + y^2 = 1 or x^4 + y^4 = 1, it is more likely a square and the intervals are the same for three of them (from -1 to +1).
![]()
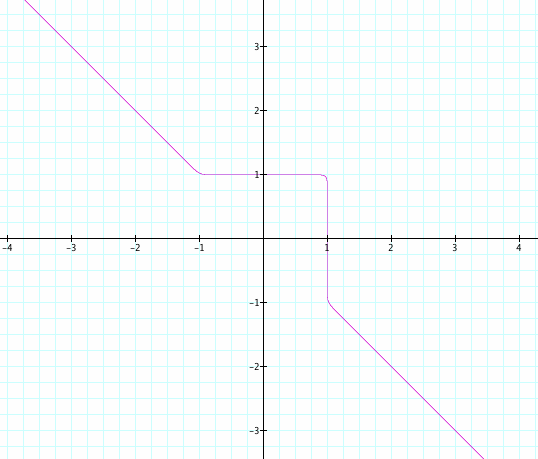
As I expected, the graph looks line y=-x except the interval from -1 to +1. Compare to x^3 + y^3 = 1 or x^5 + y^5 = 1, it is getting closer to y=-x function in the second and fourth quadrant and a square in the first quadrant.