

Assignment 2:
Quadratic Equations
by:
Sarah Link
The Problem:
Graph the parabola: ![]()
i. Overlay a new graph replacing each x by (x-4).
ii. Change the equation to move the vertex of the graph into the second quadrant.
iii. Change the equation to produce a graph concave down that shares the same vertex.
iv. Generalize...
The Investigation:
First things first, we need to graph the parabola given in the problem.
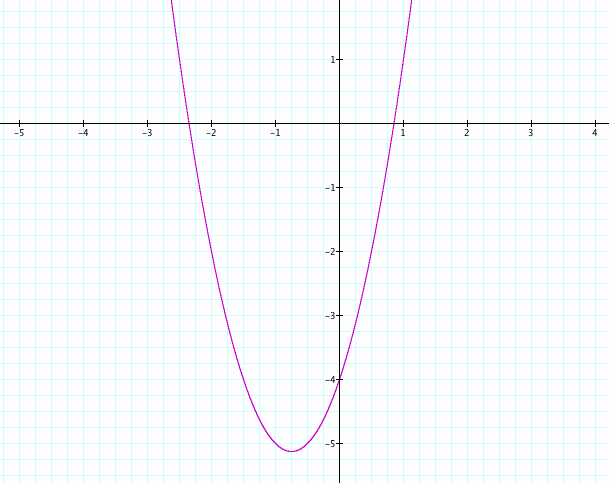
We can see that it is an upward facing parabola. If we think back to our general quadratic equation of ax^2 +bx + c here a = 2, b = 3, and c = -4. The parabola is compressed horizontally shifted to left and shifted down. What we want to explore next is changes to this graph.
i.
We want to replace all the x's with (x-4). We can try and predict what this will do to the graph. If we have the line y = x, and change it to y = x - 4, our line will be shifted down by four units. If we have y = x^2, and make it y = (x - 4)^2, the parabola will be shifted 4 to the right. So when we replace our given equations with (x - 4), we can predict that a shift of four units will occur, the question is in what direction?
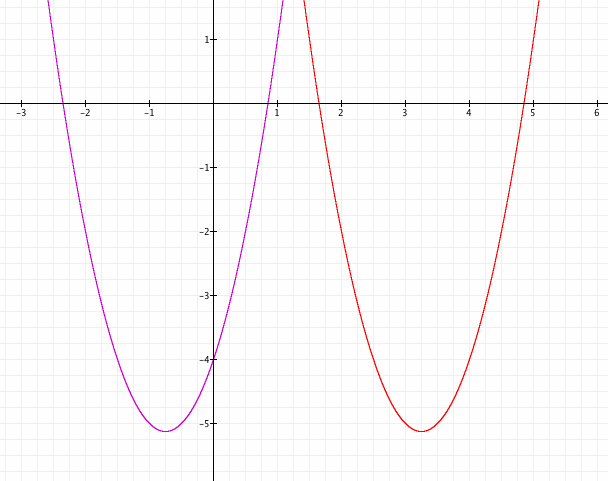
We see that when we change x to (x - 4) we were correct in our conjecture that it would shift by four units. It has shifted right four units and seems to have remained unchanged otherwise.
ii.
We are trying to move our vertex into the second quadrant. We see that changing our x value by a constant moves it left or right, we need to investigate how to move it up or down. From our original equation we need to move the parabola up by a little over 5 units. We know that adding or subtracting a constant to a parent equation will shift the equation vertically so we will start by looking at our c value.
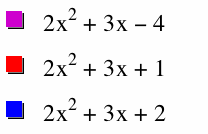
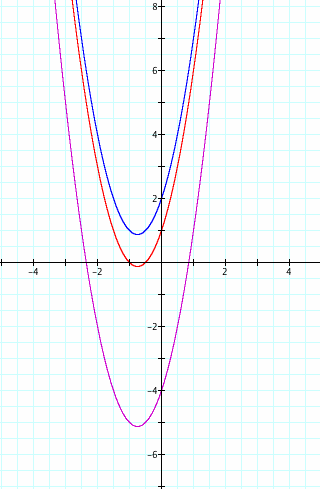
We left our original equation graphed in purple. We first change c to +1 since we estimated it needed to be moved about 5 units up. As we can see from the red parabola, this gives us a vertex that is still slightly too low. So we change c to +2. The blue graph clearly gives us vertex that is placed in the second quadrant.
iii.
We are now given the task to keep our vertex the same, but transform our parabola into one that is concave down. We know that if we are given y = x and we change it to y = -x it reflects the graph over the x-axis. We also know if we have y = x^2 and we change it to y = -(x^2) it also reflects over the x-axis. So let us first attempt to simply place a negative in front our new found equation (we will work off the one graphed in blue above).
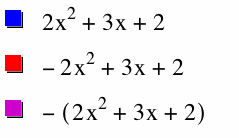
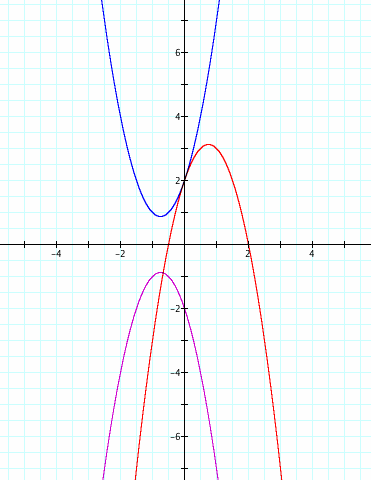
We attempted placing a negative in front of the 2 and then also placing a negative in front of the entire equation. Niether of these did what we wanted but they produced some interesting results. The negative solely in front of the 2 flipped the parabola to become concave down but also shifted it vertically upward. It appears to have reflected our original graph over the line y = 2. When we tried putting the negative in front of the entire equation it reflected it over the x-axis. We want the purple graph, but we need it shifted up what looks like two units in order to keep the same vertex as our original equation. Let's test this theory:
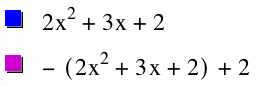
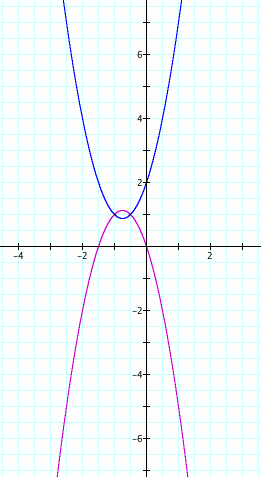
We see from the above purple graph that we overshot our vertex. We can now use the formula we know to find the y coordinate of the vertex of our blue parabola. The equation for y - coordinates is c - (b^2/4a) so from our blue equation y = 2 - (3^2/4*2) = 2 - (9/8) = (16-9)/8 = 7/8 = .875. Knowing this we can go back to equation that reflected our blue parabola over the x axis and can conclude that the vertex of this reflected parabola has a y - coordinate of not (7/8) but -(7/8). So to move the vertex up to our blue vertex, it must be moved not 2 units up, but 2*(7/8) units up. We see this below:
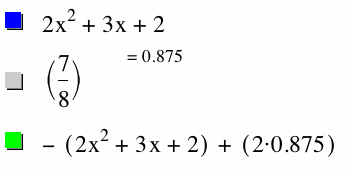
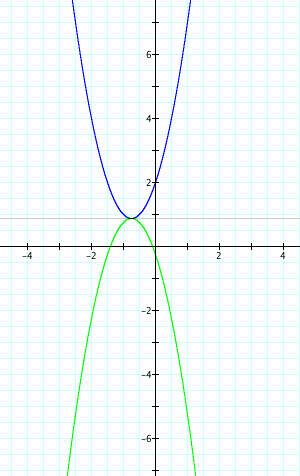
iv. Generalize...
After the above explorations it is now time to reflect back on what we can generalize about quadratics, their equations, their graphs, and how changing one affects the other. We see that placing an additive constant within the x term moves our left horizontally shifting it left and right. This was seen when x was replaced by (x-4) which exemplified the movement of four units right of our original graph. We also played around with shifted the graph vertically up and and down and discovered to do so we simply needed an additive constant on the end of our equation. Finally we went into two ideas, the concept of flipping a parabola and also the logic behind where a vertex point lies. To flip the parabola we simply needed a negative multiplicative in front of our equation, but a negative alone with reflect our original over the x-axis rather than at its own vertex. To make sure they are tangent at their vertices, we must vertically shift the reflected parabola. In order to discover how many units, we simply calculated the y-coordinate of our original vertex, multiplied it by two, and let this be our additive constant at the end of our equation. The formula for finding this y-coordinate is simply looking at our original equation and calculating c - (b^2/4a). Overall we have seen that by changing components of our equation, we are able to manipulate the graph in order to fit our desired picture.