

Friday the 
by
Amanda Newton
There only 7 different cases to examine: when the year (January 1st) begins on a Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, or Saturday.
We need to recall the amount of days in each of the twelve months. To keep things simple, let's use mod7 for each day of the year. So 1mod7 represents Sunday, 2mod7 represents Monday, . . . , 7mod7 represents Saturday. For my first attempt to understand this problem, I used an Excel spreadsheet. The first two columns including January and February are shown below.
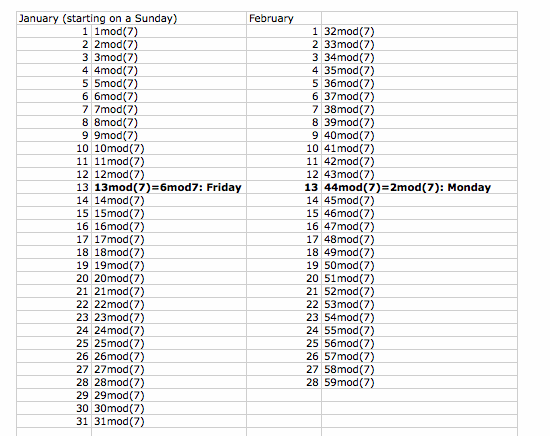
This was getting much too tedious though, so I turned to a different approach. Since we are starting on a Sunday, then the 13th will be 13mod7=6mod7. Since January has 31 days, we will add 31mod7=3mod7 to 6mod7 which will give us 9mod7=2mod7. This gives us the day for February 13th (Monday). I continued with this method (for months with 31 days - add 3mod7, 30 - add 2mod7, and for 28 days add 7mod7 (or 0mod7). The results for a year beginning on a Sunday are shown below.

The same thing can be done with the remaining 6 possibilities (the first of the year beginning on a Monday, Tuesday, etc...). However, this is unnessecary because we can see from the list above that every day (Sunday through Saturday) occurs at least once, and up to three times. If we start on a Monday, then the days above are shifted down once. No matter what day we start with, we will have the same list of numbers. Friday is just one of these days and therefore Friday the 13th will occur at least once and up to three times.
But what about the leap year?!! Will this still be the case? To see, let's generate another list using the same method above, but this time we will be adding 1mod7(29mod7) after February since it now has 29 days.
Consider the case, that January 1st will be a Sunday:

For the same reasoning we used in the regular calendar year, we can conclude that Friday the 13th will occur at least once in the leap year and up to 3 times per leap year.
* Prove that Friday the 13th can occur in two consecutive months only in February and March in a year that is not a leap year. On what day of the week must January 1 occur for February and March to have Friday the 13ths?
Since there are only 7 cases for each year and leap year, we could certainly create 14 lists in a relatively small period of time consisting of every possible scenario concerning Friday the 13th. But let's remember a very important aspect of proof - the only proof that can be given by an example is a counterexample, which is to some a debateable form of proof. Instead, let's reason through our lists. First consider our list from the regular calendar year.

Notice the only consecutive months having the same day of the week for the 13th are February and March. So if we began the list considering January 1st was a Monday, rather than a Sunday, each of the days in the list above would be instead the following day (i.e January: Saturday, February: Tuesday, etc..). The case then for when Friday the 13th occurs for two consecutive months can only occur in February and March. This case will actually happen when January 1st is a Thursday. I know this because in our original list, Monday occurs consecutively, so adding 4 days would place us on two consecutive Fridays. So we then add 4 days to our starting date which was Sunday so we must start on a Thursday.
Note: the same argument follows for any day of the week. We can replace Friday with Wednesday - that is, Wednesday will only occur on 13th of 2 consecutive months for February and March.
Why is it that the 13th of every February and March falls on the same day of the week for regular calendar years? Recall the math involved to generate our list. Once we have the mod corresponding to the day of the week for February 13th, we add 0mod7 (this is equal to 7mod7) to get mod corresponding to the day of the week for March 13th. Adding 0mod7 in modular arithmetic is equivalent to adding 0 in classical arithmetic. Adding zero does not change anything - so we are left with the same modular value in March as we had in February.
We have only proven that the only months in which Friday the 13th can occur consecutively are February and March for regular/non-leap years. This should now be easy to see. Recall our list made in reference to the leap year beginning on a Sunday.

As we can see, there are no consecutive months in which a day of the week occurs twice. (This is because we no longer add 0mod7 because there are now 29 days in February (1mod7). Using the same argument above, then, there will never be a Friday 13th for two consecutive months during a leap year.
That's okay with me; they are unlucky anways - the less the better!
*Observe that in 1998, both February and March have a Friday the 13th. What is the next year in which this will occur again?
An immediate (but incorrect) response to this question may be:
February and March will both have a Friday the 13th again in 7 years, so 1998 + 7 = 2005. This answer is ignoring the existence those pesty leap years. We need to take these into consideration before recalculating.
Leap years were introduced in the Julian calendar in 46 BC and have been occuring every 4 years since. The Gregorian calendar (most widely used) recognizes a leap year for every year that is a multiple of 4 with the exception of years that are divisible by 100 but not 400 (i.e. 1700, 1800, 1900) (Wolfram.com).
Returning to our problem, we can find the nearest leap-year to 1998 using this new information provided. We have already shown that 1998 cannot be a leap year because February and March have the same day of the week on the 13th. We can also infer this because 1998 is not evenly divisible by 4. 1996 must be a leap year and hence, so is 2000, 2004, 2008, etc... In 1999, February and March the 13th will fall on a Saturday. The year 2000 is a leap year so February the 13th will fall on a Sunday and March the 13th will fall on a Monday. Three years later (2003), they will both fall on a Thursday (since Thursday is three days later that Monday). In 2004, we encounter another pesty leap year so only February the 13th will fall on a Friday, and March the 13th will fall on a Saturday. 2008 is another leap year, so February the 13th will fall on a Wednesday, and March the 13th will fall on Thursday. Therefore, the next year, 2009, February and March will both have a Friday the 13th. The famous horror movie, Friday the 13th, was re-released in 2009. Coincidence? I think not.
Rather than going through the same cycle to find when this will happen after 2009, is there a pattern? Can we determine which years between 2000 and 2100 this will occur?
The years between 2000 and 2100 where Friday the 13th will occur in February and March will be 2009, 2015, 2026, 2037, 2043, 2054, 2065, 2071, 2082, 2093, and 2099. By looking at the differences, we reveal the pattern:
6, 11, 11, 6, 11, 11, 6, 11, 11, 6
At first there is a six year difference, then an eleven year difference twice, and this pattern repeats itself throughout the years 2000 and 2100. Will it continute to repeat itself past the year 2100?