

The Pythagorean Theorem: Its Importance in Mathematics and a Teaching Approach
by
Amamda Newton
Promoting conceptual understanding is a growing focus in the teaching of mathematics. Research continues to show that conceptual learning, rather than solely procedural based learning, leads to a greater overall understanding of the subject material (NCTM, 2000). There are numerous ways teaching the Pythagorean Theorem conceptually. Too often, teachers resort to simply giving their students the formula ![]() with little or no reasoning involved. The theorem, however, is much too essential to mathematics to be taught procedurally. Students need to be introduced to the material through concrete tasks, followed by abstract applications of the concept. It is essential for the students to be able to apply their formulaic knowledge to different types of situations.
with little or no reasoning involved. The theorem, however, is much too essential to mathematics to be taught procedurally. Students need to be introduced to the material through concrete tasks, followed by abstract applications of the concept. It is essential for the students to be able to apply their formulaic knowledge to different types of situations.
Teachers should begin their lesson sequence with concrete tasks, allowing their students to become comfortable with the information before moving to the abstract concepts. By introducing the foundational formulas and ideas, the teacher is setting their students up for success. Studies have shown that not introducing mathematical concepts with concrete instruction lowers the overall understanding of the materil (Butler, Miller, Crehan, Babbitt, & Pierce, 2003). To begin the lesson, the teacher should introduce the history of Pythagorus, making sure to allow the students to provide any information they may already know. After briefly discussing the background of Pythagorous, his theorem can be introduced. The full theorem should be written on the board, and time should be given to allow students to try and explain it in their own words. Clearly this dicussion should be monitored to avoid any misinterpretations of the theorem. The instructor should also make sure students are comfortable with the definitions of right, acute, and obtuse triangles as well as the terms leg and hypotenuse.
Once the topic and theorem have been introduced, the students should explore some examples. A handout with constructed triangles should be given out in which students have to document the length of each side of the triangle, calculate the square of each side, and calculate the sum of the squares of the two legs of each triangle. The constructed triangles should be acute, right, and obtuse. Rulers or other measuring devices should be distributed along with the handout. The teacher should then ask the students what they discovered about the theorem. By comparing the sum of squares of the sides to the hypotenuse of each of the triangles, the conclusion of the exercise should be the understanding that the theorem dows not hold for acut or obtuse triangles. It can be shown more clearly that the theorem does not hold for non-right triangles using the Law of Cosines. Unfortunately, this topic is not introduced until Accelerated Math III or Math IV. An important point to make at the end of this exercise is that a theorem can never be proven by just a few examples (or many). However, providing a counterexample or obtuse and acute triangles does indeed show that the theorem does not hold for non-right triangles.
Now that the theorem has been introduced and somewhat explored, students should be presented with the conceptual proof. To fully understand this task, students should be comfortable with finding the area of rectangles as well as triangles. This knowledge should have been solidified in ealier grades, but a small review may be necessary. The Georgia Performance Standards (GPS) and the National Council of Teachers of Mathematics (NCTM) Principles and Standards both require that students in grades 6-12 be able to "recognize reasoning and proof as fundamental aspects of mathematics" as well as "develop and evaluate mathematical arguments and proofs" (National Council of Teachers of Mathematics, 2000). This task will address each of these standards.
Figure I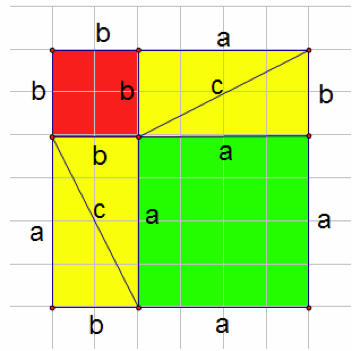
Figure II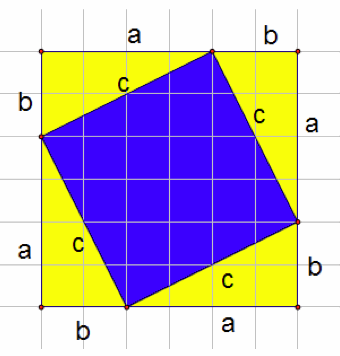
Using figure I, have students find the area of the green and red squares as well the yellow rectangles. They should easily deduce the area of the green square is ![]() , the red is
, the red is ![]() , and each rectangle has an area of a*b. From here, they should calculate the total area of the larger square in Figure I which is the sum of each of the smaller areas:
, and each rectangle has an area of a*b. From here, they should calculate the total area of the larger square in Figure I which is the sum of each of the smaller areas:
![]() =
=![]()
The instructor should then lead them to find the area of the yellow triangles and the 'tilted' blue square in Figure II. They will find the area of the blue square is ![]() and each of the four yellow triangles has an area of (1/2)(a*b). The total area of the square in Figure II then is
and each of the four yellow triangles has an area of (1/2)(a*b). The total area of the square in Figure II then is 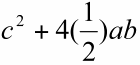 =
= ![]() . If it has not already been addressed, recognize the two larger squares in Figure I and Figure II are equal, since each have a side length a+b. Therefore
. If it has not already been addressed, recognize the two larger squares in Figure I and Figure II are equal, since each have a side length a+b. Therefore ![]() =
= ![]() . The most important point to make here is that sides a and b are also the sides of the right triangles in each figure, and c is the hypotenuse of each triangle. The students should be answering all of these questions and the teacher should act as a prompter.
. The most important point to make here is that sides a and b are also the sides of the right triangles in each figure, and c is the hypotenuse of each triangle. The students should be answering all of these questions and the teacher should act as a prompter.
The proof task is critical because the student learns to build on previously, and more foundational, mathematical concepts, which is an essential aspect of mathematics. The Georgia Performance Process Standards require that students "understand how mathematical ideas interconnect and build on one another to produce a coherent whole." In the task, the students have essentially proven the theorem on their own, which builds their confidence and understanding of the material. The Georgia Performance Standards also state that eighth grade students should "recognize and interpret the Pythagorean Theorem as a statement about areas of squares on the sides of a right triangle." The proof shown does exactly this.
One of the benefits of figure II being shown on a graph is that the demonstration of the distance formula can be derived directly from the same picture. The Georgia Performance Standards for Math I (9th grade) states students should "understand the distance formula as an application of the Pythagorean Theorem." We have already shown the relationship between sides a, b, and c. Now, if we attach coordinates to each point, students can use the same mathematical reasoning to deduce the distance of ![]() must be the same as the distance of
must be the same as the distance of ![]() . By simple Algebra and with an explanation of finding the distance of sides (the difference in the x-coordinates, and the difference in the y-coordinates), it can be reduced to the distance formula. It is clear that the reasoning used in the proof task for the Pythagorean Theorem sets the foundation for the distance formula and shows their direct relation.
. By simple Algebra and with an explanation of finding the distance of sides (the difference in the x-coordinates, and the difference in the y-coordinates), it can be reduced to the distance formula. It is clear that the reasoning used in the proof task for the Pythagorean Theorem sets the foundation for the distance formula and shows their direct relation.
The next task is more interactive and technology-enhanced. NCTM and the Georgia Performance Standards both call for the use of technology in math classrooms to enhance and engage student learning. In this task, students will once again fulfill the Geometry standard for eighth grade mathematics to relate the area of squares on the sides of a right triangle to the Pythagorean Theorem. The applets will allow students to manipulate objects to again see the truth and meaning in the Pythagorean Theorem. There is a multitude of applets available at no cost online, and many of them can be constructed in Geometer's Sketchpad.
An excellent site which features numerous applets, activities, and lessons on the Pythagorean Theorem is internet4classrooms.com. Several of the applets listed provide excellent demonstrations of the Pythagorean Theorem.

Figure III
Click here to see or play with this applet
Figure III shows the image of an applet provided by the website which allows students to shift, rotate, and move the red and green squares, while preserving their areas, so that they both fit into the empty larger square. Each of the applets provides instructions for the students. The applet shown below (Figure IV) allows students to change the size of the inner right triangle, which then alters the size of each of the three squares. From this point, they are instructed to drag each of the five pieces in a way that they fit into the larger square.

Figure IV
Click here to see or play with this applet
An applet from pbs.org in figure V (below) instructs students to try similar methods as described for applets in figure III and IV, but instead focuses on unit squares. The student can arrange each individual unit square from the green and blue squares to fit into the larger white square.

Figure V
Click here to see or play with this applet
The instructor can split students into small groups, each exploring the theorem through a different applet. After an appropriate period of time, each group can demonstrate their applet to the class and explain why the shapes fit, and how it displays the Pythagorean Theorem. Interactive learning helps solidify the students' understanding of the concept. They may have already been sure the shapes would fit, but actually trying for themselves and being able to manipulate the shapes will help them retain the newly learned information.
Now that students have been introduced to the Pythagorean Theorem and experienced it for themselves, they can apply this information more generally. At this point, students should understand the abstract applications of the theorem in addition to the concrete examples and terminology. A grasp of the abstract ideas will make the students much more capable of applying the Pythagorean Theorem to examples of any form. This will address another Georgia Performance Standard stating students in eighth grade mathematics should "apply properties of right triangles, including the Pythagorean Theorem" (Georgia Department of Education, 2005). Students should now be given an opportunity to demonstrate their knowledge and understanding of the material through application, as slowly building on previously learned material enhances student confidence and leads them to engage in mathematics more frequently. After finishing the proof task, the instructor should ask, "How can we use the Pythagorean Theorem?" The instructor should construct a right triangle on the board and label the two legs. The students should then be asked to calculate the hypotenuse. For example, given the picture below, find the missing value for the hypotenuse "c."
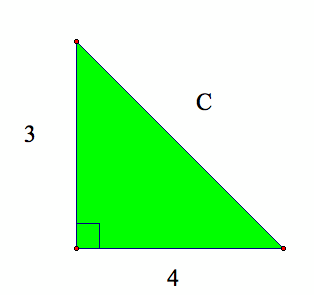
The solution should be quite simple for students. Using the Pythagorean Theorem, ![]() , so
, so ![]() . They should try some other examples where the hypotenuse and only one side of the triangle are given. Students will be applying the Pythagorean Theorem while also practicing solving equations for a given variable, both of which are important to Georgia Performance Standards for both middle and high school level mathematics.
. They should try some other examples where the hypotenuse and only one side of the triangle are given. Students will be applying the Pythagorean Theorem while also practicing solving equations for a given variable, both of which are important to Georgia Performance Standards for both middle and high school level mathematics.
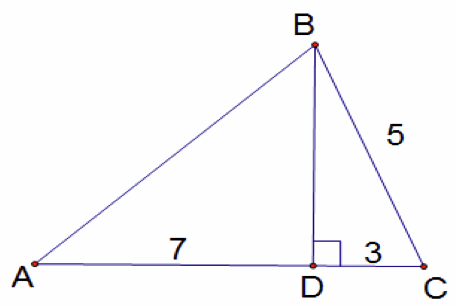
From here, students have been fully introduced to the concepts of the Pythagorean Theorem. Students should try a few more basic problems as well as problems requiring them to calculate the area of the triangle using the Pythagorean Theorem. In the diagram below, students can be asked to find the area of triangle ABC. To do so, they must use the Pythagorean Theorem to find the height BD.
The tasks are setting these students up for high school level mathematics and reasoning. Now, most importantly, the instructor should provide more worthwhile examples with real life applications of the Pythagorean Theorem, which are plentiful. For example, ask students to solve the following problem:
The cross-country team leaves the school and runs due south for 5 kilometers, they then turn and run due west for another 8 kilometers. What is the shortest possible distance they will have to travel to get back to school? (Round to the nearest hundredth)
A picture should be drawn by students to illustrate the problem and so they can see the relationship involved. Their answer will be ![]() kilometes. A great homework assignment that can be a supplement to all of these tasks would be to have students write and solve their own problem, which includes a real life application of the Pythagorean Theorem. They should be encouraged to write difficult problems that include multiple math concepts or that might stump their peers. On the following day, students can exchange or present problems to the class.
kilometes. A great homework assignment that can be a supplement to all of these tasks would be to have students write and solve their own problem, which includes a real life application of the Pythagorean Theorem. They should be encouraged to write difficult problems that include multiple math concepts or that might stump their peers. On the following day, students can exchange or present problems to the class.
The tasks described address many of NCTM and Georgia Performance Standards. They also help build a solid foundation of the Pythagorean Theorem which is extended at the high school level. High school topics that use the Pythagorean Theorem include the distance formula (as mentioned earlier), congruence postulates and special right triangles (Math I), trigonometric ratios and functions (Math I and Accelerated Math III), relationships between lines and circles (Math III), conics (Math III), and many more. Through the sequence of tasks provided, students will "reason and evaluate mathematical arguments," "solve problems (using appropriate technology), "communicate mathematically," "make connections among mathematical ideas and to other disciplines," and "represent mathematics in multiple ways" (Georgia Department of Education, 2005). All of the middle and high school process standards are addressed in the tasks, and are enhanced as a result of the particular sequence in which the tasks are given.
If you are interested in a lesson plan, rather than an essay, click here
References


