

Assignment 6
The Medial Triangle
by
Kaitlin Spooner
Given three line segments j, k, and l that are the side lengths of the medial triangle, construct the triangle. Once we have constructed this triangle, can we construct the parent triangle of this triangle? What is the relationship between the original medial triangle and the second parent triangle that we constructed?
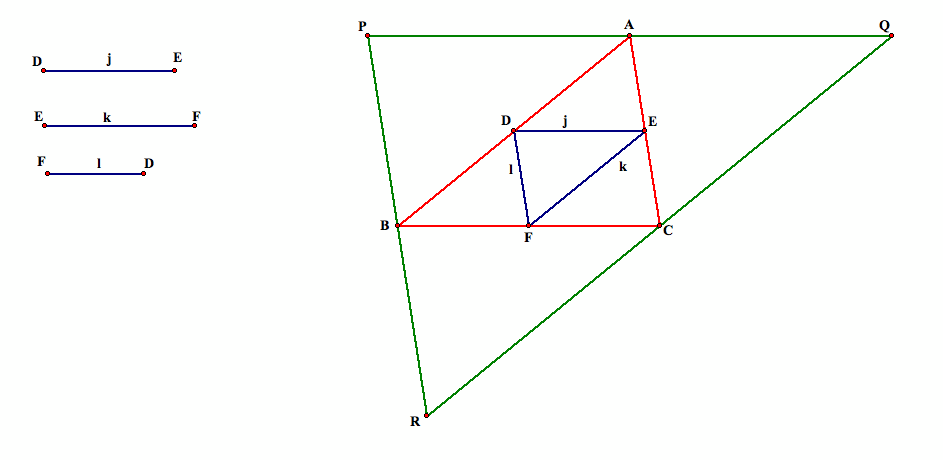
We are given three sides of a medial triangle, j, k, and l, and we want to construct the original triangle. First, say we have the original triangle. How do you construct the medial triangle? Find the midpoint of each side of the triangle. Connect each of these midpoints to form a triangle which is the medial triangle. Below, the original triangle ABC is shown in blue, and the medial triangle DEF is shown in red. By construction, we know that segment AD is congruent to segment DB, segment BE is congruent to segment EC, and segment CF is congruent to segment FA.
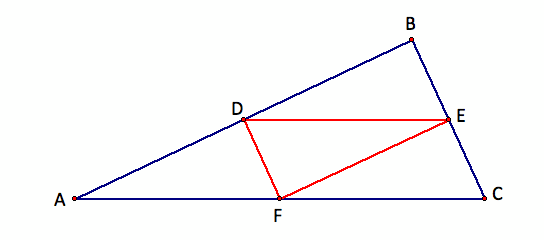
So now what happens if we only know the lengths of the sides of the medial triangle? By theorem, we know that a point D is the midpoint of a segment AB and a point E is the midpoint of segment BC, the segment DE is half the length of the segment AC and DE is also parallel to AC. This theorem will be crucial for our construction.
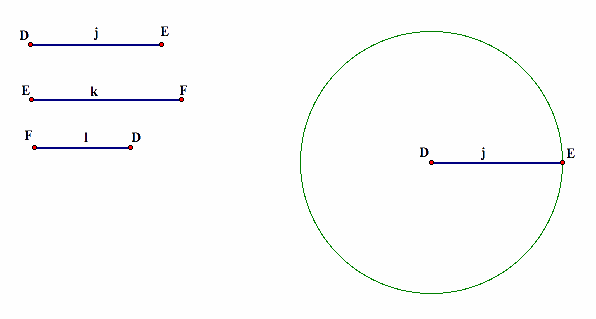
First, let's begin with the three lengths of the sides of the medial triangle. We want to copy the first segment j, so construct point D, and construct a circle with center D and radius j.
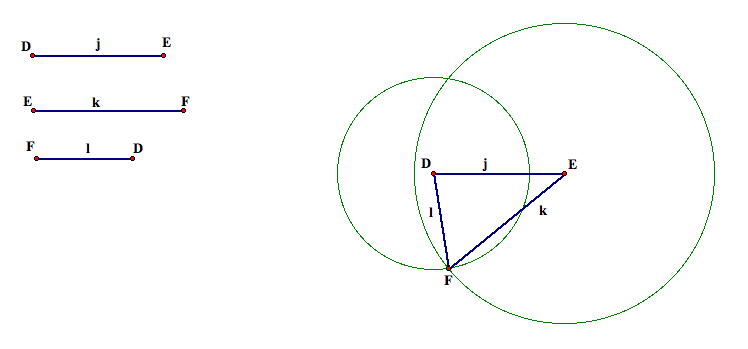
Next, we want to copy segments k and l in such a way that j, k, and l form a triangle. To do this, we construct a circle with center D and radius l, and we construct a second circle with center E and radius k. The point where these circles intersect is point F, so we can construct the medial triangle by constructing segment l from D to F and constructing segment k from E to F.
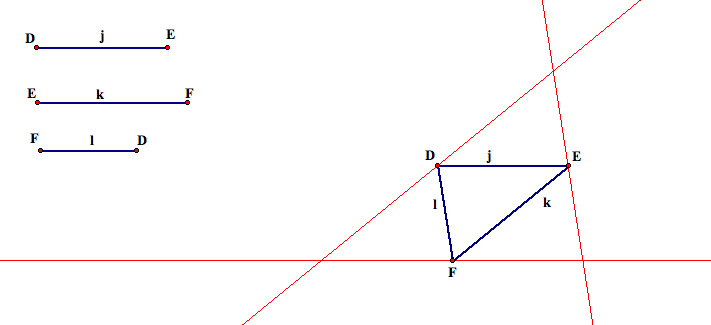
Now, we want to begin constructing the original triangle. Since we know by definition of the medial triangle that each vertex of a triangle lies on a side of the original triangle and that a side of the medial triangle is parallel to the side of the original triangle that is opposite of it, we can construct a set of parallel lines. For example, we will construct a line through point F that is parallel to segment j. We will also construct a line through E that is parallel to l and a line through D that is parallel to k.
These lines form the sides of our original triangle. Construct points A, B, and C at the intersection of these parallel lines and construct segments AB, BC, and CA. We now have our original triangle ABC which is shown in red.
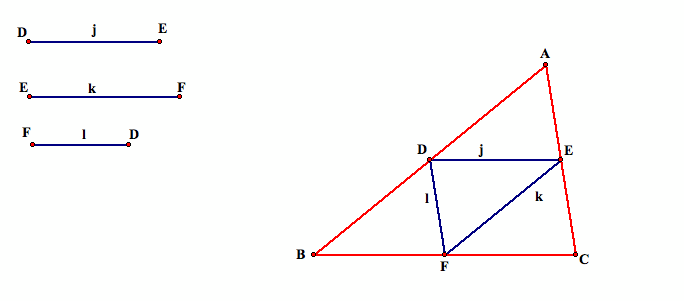
Now we can check our construction to see if our construction is correct. First, we will check that D, E, and F are midpoints of the segments of our original triangle. For example, segment AD must be congruent to segment DB.
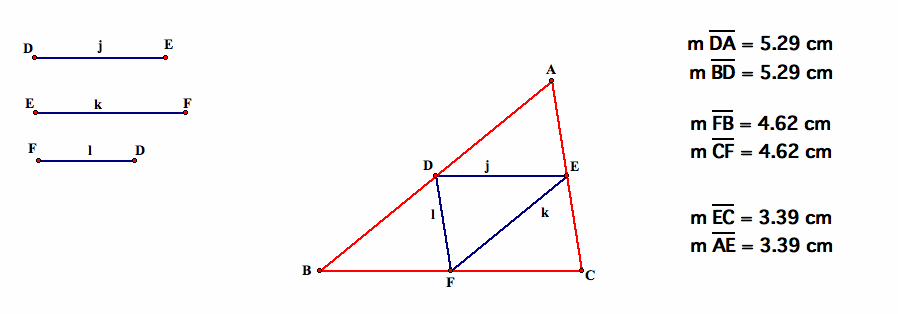
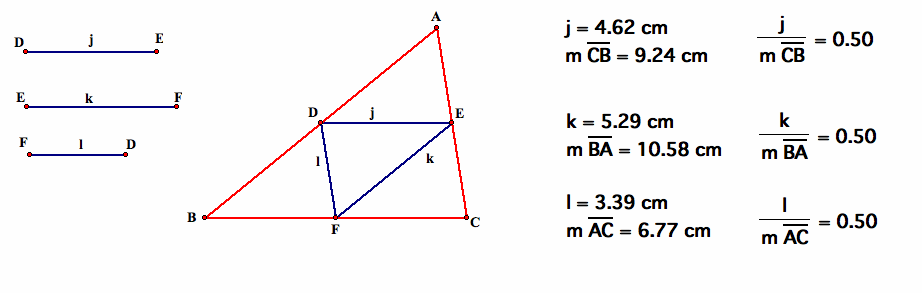
We can also check our triangle by using the theorem. Segment j must be half the length of segment BC, so the ratio of j over BC must equal one-half, or .5. This should hold true for each other set of the sides of our triangles: k pairs with AB, and l pairs with CA.
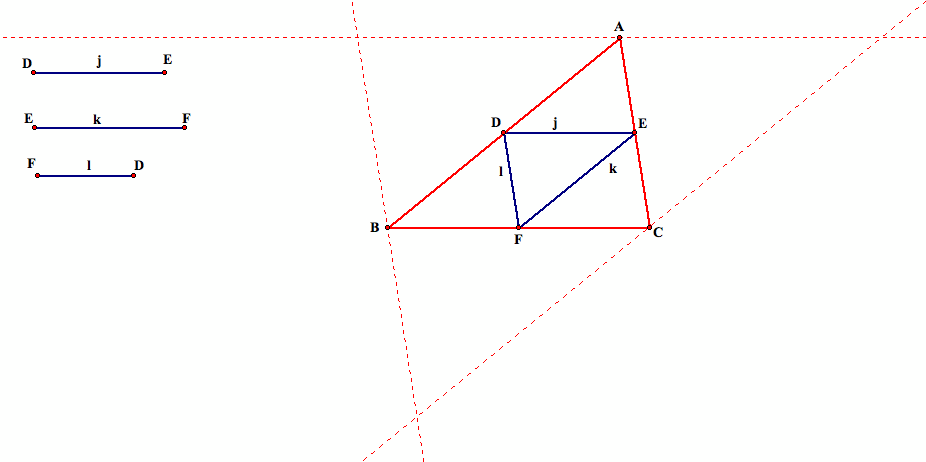
Want to explore the medial triangle and this construction more? What does the original triangle look like when we start with different lengths for the medial triangle? Click here for a Geometer's Sketchpad script tool that you can use to construct the original triangle from the side lengths of the medial triangle.
Now we have the original triangle, which we will call the first parent triangle. What if we wanted to construct the second parent triangle? This is a triangle whose medial triangle is the first parent triangle. To complete this construction, we can use the same theorem as before. Construct parallel lines similar to the previous construction. For instance, construct a line through A and parallel to BC. Do this for each vertex on our first parent triangle.
The points where these lines intersect are the vertices of our second parent triangle. Given the side lengths of the medial triangle, we now have the first parent triangle ABC and the second parent triangle PQR shown in green. In summary, triangle DEF is the medial triangle of triangle ABC, and triangle ABC is the medial triangle of triangle PQR.
Want to explore the second parent of a medial triangle further? What does the second parent triangle look like when we start with different lengths for the medial triangle? How does the given medial triangle compare to the second parent triangle? Click here for a Geometer's Sketchpad script tool that you can use to construct the second parent triangle from the side lengths of the medial triangle.
What is the relationship between the given medial triangle and the second parent triangle? Side lengths, similarity, parallel sides, same orientation
Can we repeat this process to find the third, fourth, fifth, etc. parent triangles? How are they related?