Describe two lines, f(x) and g(x) such that f and g are tangent to the product h(x) = f(x)g(x).
First off, what does it mean for a line and a parabola to be tangent? After doing a Google search online, I found very few definitions that would work. So, I fall back on what I know. A line and parabola are tangent if the tangent line of the parabola at a particular point is equal to the slope of the line. In other words, the tangent line and the original line would have the same equation.
Then, I had to think about what it means for the product of two lines and the lines themselves to be tangent to each other.
Since one way of tackling a larger problem, I looked at a simpler problem. Let
Again I gnashed my teeth. The two curves, the parabola and the line, had to intersect at the same point while their tangent lines must have the same slope.
Setting f' = h', we get
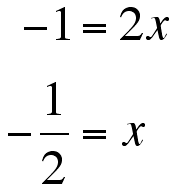
Doing the same with g' and h',
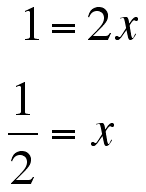
So, the two x's where the slope of the lines and the slope of the tnagent lines of the parabola are equal are at x = +/- 1/2. The other part of the puzzle is that not only must the slope of the tangent lines be equal, the also must interesect at the same point. So, the y's must be equal.
So we set up the corresponding functions and solve for c:
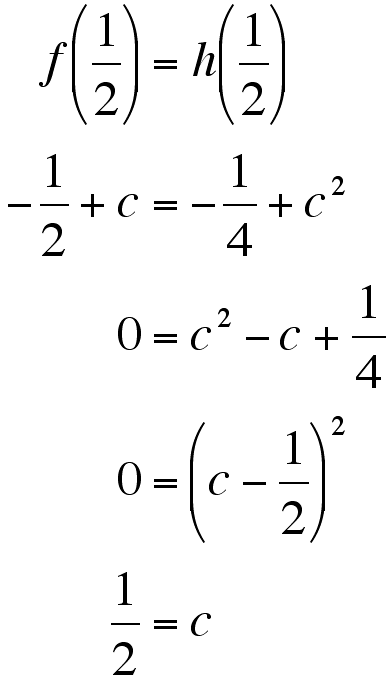
To test this, I went to Graphing Calculator and set up this picture.graphing the following equations:
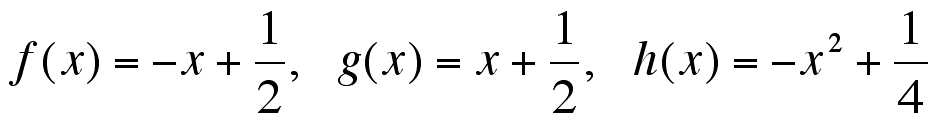
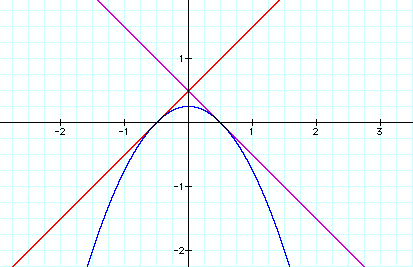
By observation, it seems as if the roots of the parabola also happen to be the points of tangency. That's interesting because, no matter what the equations are, the roots of h(x) are going to be the roots, or x-intercepts of f(x) and g(x) by the way h is built. You can click here for some examples of that idea. f and g might intersect h elsewhere, but the two roots remain a constant occurance.
Let's do this for the general case.
Given the following equations, describe when the lines are tangent to the product of themselves.
Let's start with the general case for the lines and the product:
And their corresponding derivatives:
The roots of f and g respectively are:
If we set the derivatives of f and h equal to each other at the first root, then we should find something about the constants a, b, c, and d. We hope.
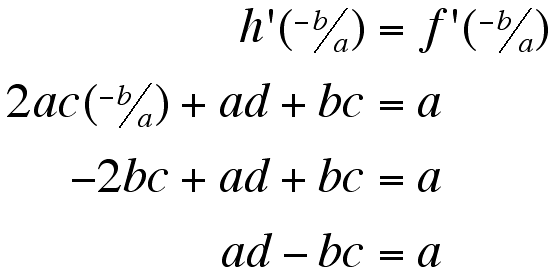
Now to do the same with the derivatives of g and h.
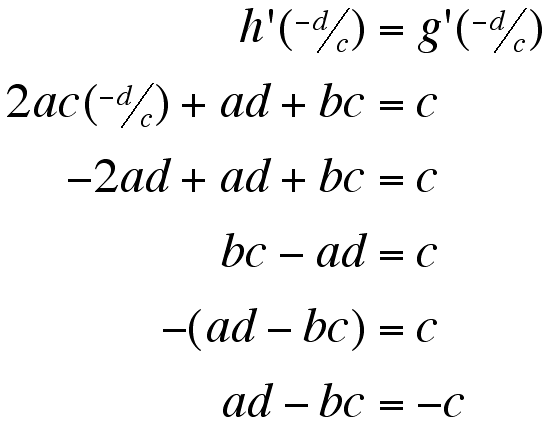
So, from the previous two equation sets and substituion we get
Substituting again, we get
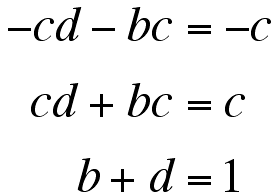
So, a and c must be opposites, and b and
d must add to 1. Picking various values for a and
c, we can generate b and d and test to see
if this holds. Here
is a generic Graphing Calculator script for doing just that. Be
sure to change the values for a and b. Trace to
the roots of the polynomial. Does our prediction for the roots
hold true?
Graphing Calculator is a product of Pacific Tech.
Follow up questions:
1) Will we ever have a parabola that opens up and still be tangent to f and g? If yes, how so? If no, what could you do to change either f, g, or h to get a parabola opening upwards, even if it's not the product of f and g?
2) Is there a way to generate a sideways parabola from h that would be tangent to f and g?
This page last modified 14 October 2002. And, brother, it needs more modifications.