

Jackson Huckaby
Euler's Theorem.
Now that students have constructed their tetrahedrons, we will move on to a discussion about properties of a three deminsional object. The three aspects we will be considering will be:
Number of Faces (F),
Number of Vertexes (V),
Number of Edges (E).
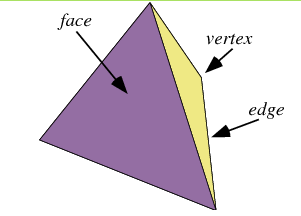
The face of a polyhedron is one of the flat surfaces that make up the polyhedron. Each face of a polyhedron is made up of a polygon.
An edge of a polyhedron is the line segment created where two of the faces of the polyhedron meet eachother.
The vertex of the polyhedron is a point at which three or more edges meet.
Have students begin with their tetrahedron and create a chart for the # of faces, # of edges, and # of vertexes.
They will find:
| Shape | Faces | Vertices | Edges |
|---|---|---|---|
Tetrahedron |
4 | 4 | 6 |
Now, have students open Cabri 3D and have them complete the chart for the following shapes:
Cube,
Pentagonal Prisim
Square Pyramid
Octahedron
Icosohedron
Dodecahedron.
| Shape | Faces | Vertices | Edges |
|---|---|---|---|
| Tetrahedron | 4 | 4 | 6 |
| Cube | |||
| Pentagonal Prism | |||
| Square Pyramid | |||
| Octahedron | |||
| Icosohedron | |||
| Dodecahedron |

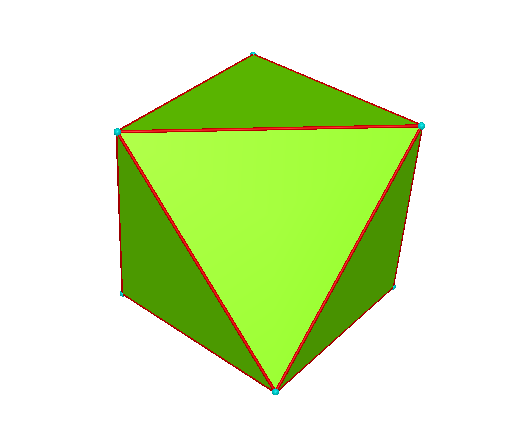
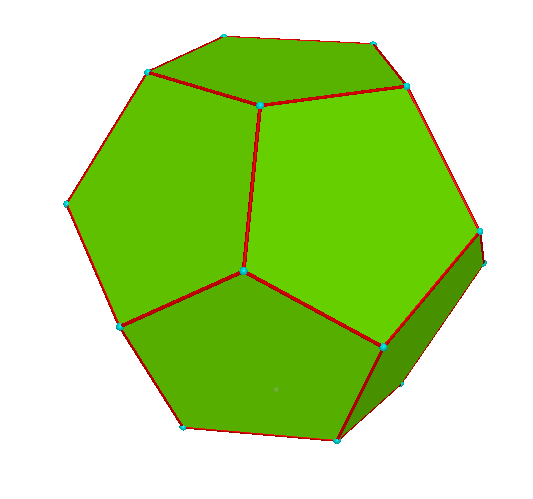
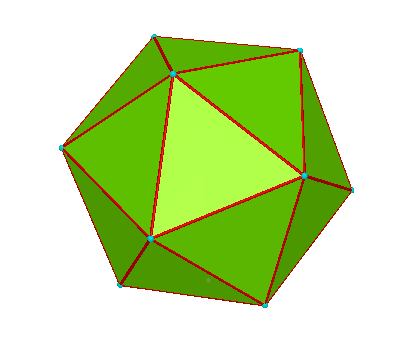
| Shape | Faces | Vertices | Edges |
|---|---|---|---|
| Tetrahedron | 4 | 4 | 6 |
| Cube | 6 | 8 | 12 |
| Pentagonal Prism | 7 | 10 | 15 |
| Square Pyramid | 5 | 5 | 8 |
| Octahedron | 8 | 6 | 12 |
| Icosohedron | 20 | 12 | 30 |
| Dodecahedron | 12 | 20 | 30 |
As students complete the chart let them feel free to create their own prisms on the Cabri software and record the information. Students should begin to try and look for the pattern that has developed.
This brings us to Euler's Formula.
Euler noticed that all of these polyhedron follow a simple rule. The number of Faces plus the number of Vertices minus the number of Edges is always equal to 2.
Or more simply:
F+V-E=2.
Have the students use the seven shapes they created to test the theorem. Have them create any convex polyhedron and test it on that as well.
This is Euler's Geometry Theorem.
Return to unit.