Jackson Huckaby
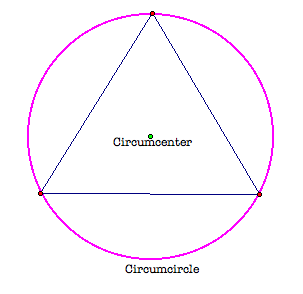
Circumcenter of Triangles
Our goal for this unit is to find the center point of a tetrahedron that will also be the center of a sphere that passes through all four of the tetrahedrons vertices. To begin the process of finding this point we will explore a 2d version of a similar scenario.
Lets begin with a simple triangle in a plane, with a goal of constructing a circle that passes through the three vertices of the triangle.
Using Geometers Sketchpad, here, try and construct a circle that will pass through the 3 vertices of each triangle.
Here are my estimations:
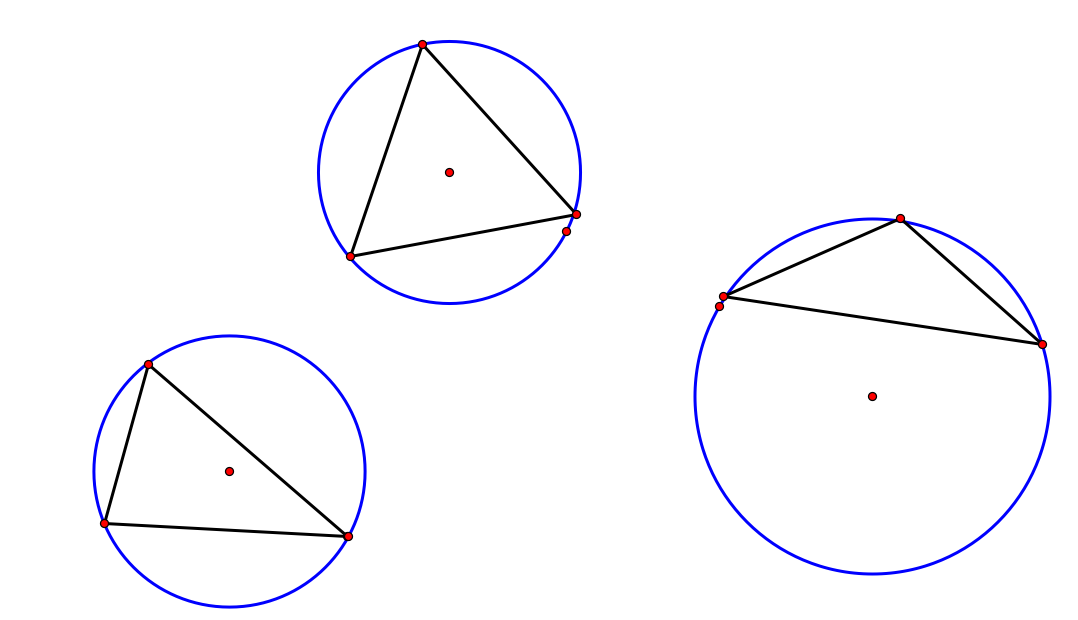
Now that we have successfully estimated our circles, we need to discover the method for finding the circumcenter of our triangles that will provide the exact center of our circumcenter!
Take a moment and look at the 3 circles above and try and come up with some construction methods that make provide us with a circumcenter.
First let us think about the geometric definition of a circle. The set of points that are equidistant from a particular point on a plane.
So if our circumcircle passes through all three vertices on our triangle, then what can be said about the center of the circumcircle?
Here's a hint:
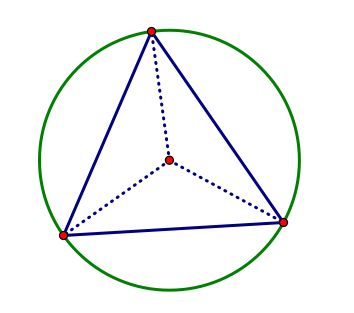
Correct! All three of our vertices will be equidistant from the circumcenter.
Using this knowledge, how can we decide how to find this center?
Lets look at triangle ABC.
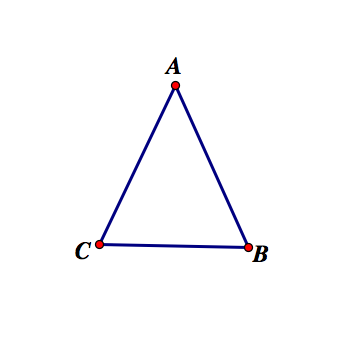
We want to find a point that is equidistant from A and B. So lets start by locating all the possible points. We will find this by first locating the midpoint between A and B, we will call this point M. This is one possible point that is equidistant between A and B. But we want all possible points. What can we do to represent them all?
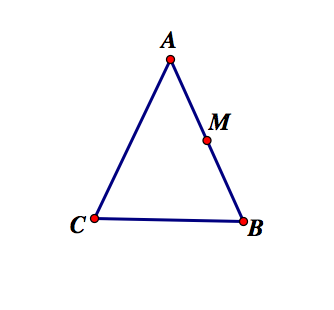
Correct! We will create a perendicular bisector through point M to line AB. An interactive example of why this creates the set of all points equidistant to points A and B can be found here.
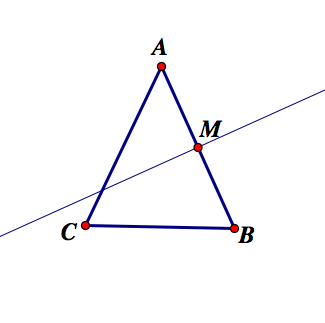
What next?
While we know our circumcircle has to be equidistant between A and B. It also has to be equidistant between A and C, as well as B and C.
So lets repeat this process for A and C.
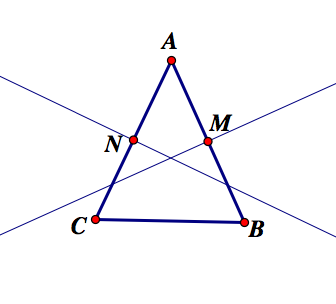
We have located our circumcenter! I chose to find the points between A and C, but B and C would have given us the same answer. If you wish to do all three perpendicular bisectors you may.
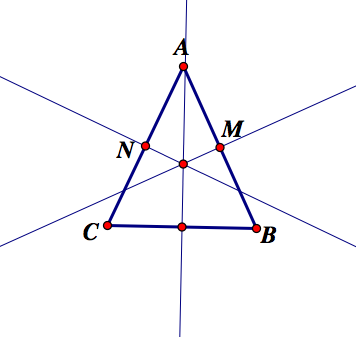
Congrats! We can now test our center by creating a circle with this point as the center (point O) and a radius of length OA. (or OB, or OC).
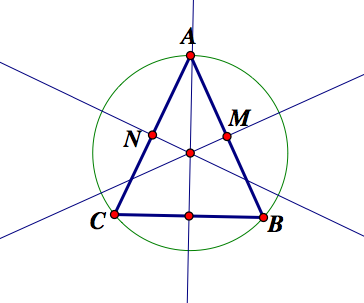
Extension.
Refer back to the three guesses we made at the top of the page. The triangle on the right's circumcenter lies on the outside of the triangle. Why is this? What other special case can you make?
Using GSP or paper and compass try and create three cases where the circumcenter is distinct.
My file can be found here.