

Assignment 1
by
Jackson Huckaby
Make up linear functions f(x) and g(x). Explore, with different pairs of f(x) and g(x) the graphs for:
i.h(x)=f(x)+g(x)
ii. h(x)=f(x)g(x)
iii. h(x)=f(x)/g(x)
iv. h(x)= f(g(x))
Summarize and illustrate.
f(x)=3x+2
g(x)=x-4
i. h(x)=f(x)+g(x)
h(x)=(3x+2)+(x-4)
h(x)=4x-2
ii. h(x)= f(x)g(x)
h(x)= (3x+2)(x+4)
h(x)=
iii. h(x)=f(x)/g(x)
h(x)=
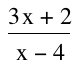
iv. h(x)=f(g(x))
h(x)=3(x-4)+2
h(x)=3x-12+2
h(x)=3x-10
An interesting GSP demonstration of the 'dynograph' of this composition can be found here.
Same procedure using different functions.
f(x)=4x+2
g(x)=2x-5
i. h(x)=f(x)+g(x)
h(x)=(4x+2)+(2x-5)
h(x)=6x-3
ii. h(x)=f(x)g(x)
h(x)= (4x+2)(2x-5)
h(x)=
iii. h(x)= f(x)/g(x)
h(x)=
iv. h(x)=f(g(x))
h(x)= 4(2x-5)+2
h(x)= 8x-20+2
h(x)=8x-18
Summary: For part i, the addition of two linear functions, we see the resulting function is also linear. This makes since because when adding functions the power will not change at all. So therefore the highest degree of the two original functions will remain the highest degree of your resulting function. Or in our case, we remain linear.
Part ii requires that we multiply f(x) and g(x). Our result we can see is a quadratic equation. The reasoning behind this is found in the exponential properties, when multiplying functions we add the exponents. So a linear function times a linear function will result in a function to the second power, or a quadratic.
In part iii we are dividing our f(x) and g(x). The result in these two situations is graphs is a reciprocal function. One with vertical and horizontal asymptotes.
Part iv is a composition of our two functions. The resulting function here is a a linear function as well. When exploring the reasoning behind this we can see that if we substitute in the a linear function for a x value of the power 1, the result will always be another linear function.