by
June Jones
Heron, or Hero, of Alexandria is credited with the first century discovery of a formula for determining the area of a triangle in terms of the lengths of the sides. Even though the formula bears his name, Arabic tradition contends that Archimedes knew and proved it much earlier.
The formula is given as:
![]()
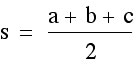
where K is the area of triangle ABC, with sides a, b, and c.
There are three common approaches to the proof of Heron's Formula. Trigonometry books usually use the Law of Cosines in the proof, and occasionally the Law of Sines. Most high school geometry books approach the proof algebraically through the Pythagorean Theorem.
We will look at the proof from a different geometrical perspective. The following constructions are performed using Geometer's Sketchpad, but the reader should feel free to use any available software (or compass and straightedge) to complete the task.
1.) Begin with any triangle, call it ABC.
2.) Inscribe a circle with center O and tangent points at D on side BC, E on side AC, and F on side AB.
3.) Extend segment CB through B to H so that HB = AF.
4.) Draw a line perpendicular to OC so that it intersects BC at K.
5.) Drop a perpendicular to BC from B; label the intersection of this line with the previous perpendicular as point L.
Your construction should look like the following:
Investigations on the way to the proof:
Again, the reader should use the tools available for the investigations.
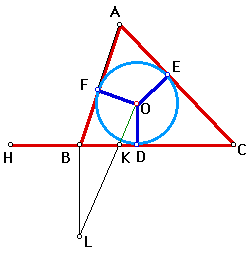
1.) Show how and why the following is true:
K = 1/2(BC)(OD) + 1/2(AC)(OE) + 1/2(AB)(OF) = (HC)(OD)
The following relationships are shown below with a measurement from GSP as an example:
1/2(BC)(OD) is the area of BOC
1/2(AC)(OE) is the area of AOC
1/2(AB)(OF) is the area of AOB
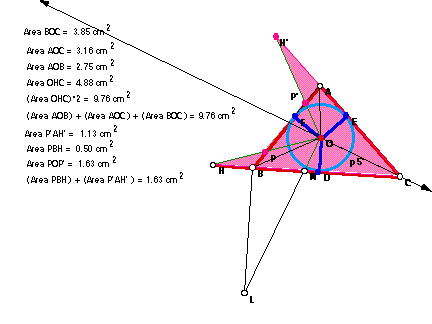
2.) Make a new figure and investigate angles:CLB, BOC, and AOF. Draw a conclusion about the relationship between CLB and AOF.
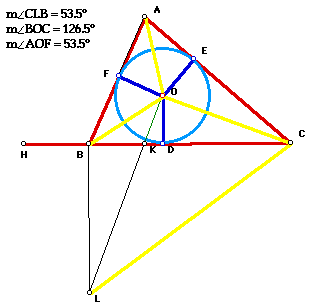
One example is shown above, but with GSP, the reader should be convinced that CLB = AOF. It might be appropriate to supply a more formal proof for this also. That task will be left to the reader.
3.) Since CLB = AOF, what can you conclude about AOF and CLB?
The reader may now use the GSP software again to be convinced that the triangles are similar. However, the "proof" of this is actually quite simple. The AA Postulate is all that is needed. The second pair of angles involved here are: AFO = CBL are right angles.
4.) Since CLB ~ AOF, the following ratios hold:
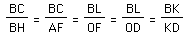
Now,
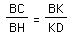 ,
so
,
so
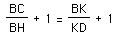 .
.
What other equality does this last statement imply?
Hint: Play around with the endpoints of the segments BC and BH. One example from GSP is shown below:
(BC/BH) + 1 = 4.45
(BK/KD) + 1 = 4.45
BC = 5.89 cm
BH = 4.45 cm
CH = 7.60 cm
CH/BH = 4.45
Hopefully, you discovered that the previous statement implied that
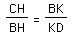 .
.
Thus
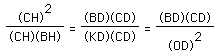
![]()
Rename AB = c, AC = b, and BC = a.
Thus we have: ![]()
Use the GSP to test this out on a triangle.
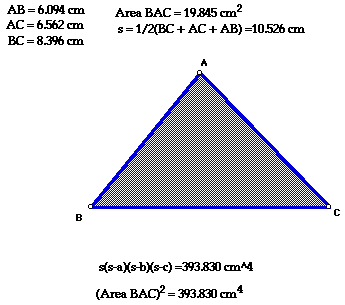
For the reader that would like to pursue this technique :
About 500 years after Heron lived, Brahmagupta gave the formula for the area of a quadrilateral inscribed in a circle as
![]()
where K is the area of the quadrilateral with sides a, b, c, and d, and
 .
.
The following is a visual example from GSP:
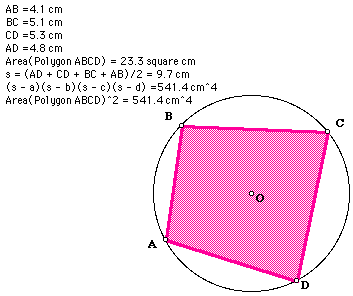
In reality, Brahmagupta's formula is more general, making Heron's formula a special case where d = 0.
One last suggestion for the reader interested in taking this just a little farther. This time let the quadrilateral have a circle inscribed and a circle circumscribed about it. (This is known as a cyclic-inscriptable quadrilateral.) Use GSP to investigate and see if you can discover an easier and shorter way to determine the area of the quadrilateral. (Solution: the area of the quadrilateral is equal to the square root of the product of its sides.)