x = t + a
y = kt + b
Lead to Linear Equations of the Form
y = mx + c
by
June Jones
EMT 668
Fall 1995
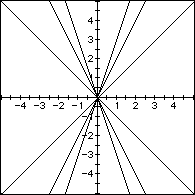
Begin with the pair x = t + a, y = kt + b by setting a = 0, b = 0, k = -3, -2, -1, 0, 1, 2, 3
and - t . Observe a family of lines through (0,0) with k equal to the slope if the line.

Thinking perhaps that k = m in general, try setting a = 2, b = 2. Again, we see a family of lines with slope of k through (2,2). Now, let k continue to be represented by the previous values and allow a b. For example, let a = 2 and b = -3. The result is the family of lines with like orientation and intersecting at (2, -3).
It can now be conjectured that m = k and (a,b) is a point of the line. In general, take the parametric form x = t + a and y = kt + b, and the rectangular form y = mx + c and substitute:
(kt + b) = k(t + a) + c
kt + b = kt + ka + c
b = ka + c
b - ka = c
Thus (a, b) is a point on the line, k is the slope of the line, and b - ka is the y-intercept.
Now use the general conclusion for a specific case:
[1] Write parametric equations of a line through (7,5) with slope 3. Graph the line using
your equations.
Solution: (a,b) = (7,5), a point of the line, k = 3, the slope
The parametric equations obtained are: x = t + 7 and y = 3t + 5
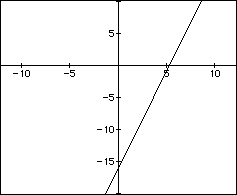
It should also be observed that the parametric equations above are not the only pair that will meet the given requirements. For example, x = t + 1 and y = 3t - 13 yield the same line. Thus the form x = t + a, y = kt + b, does not yield a unique pair. One further transformation will result in a unique pair. Since b - ka = c and c represents the y-intercept in rectangular form, set (a,b) = (0,c) = (0,b-ka). Thus the pair x = t, y = 3t - 16 would be the more general. Now x = t and y = kt + c while k is the slope and c the y-intercept.
[2] Write the equation of the line in rectangular form.
Solution: (a,b) = (7,5), m = 3, c = b - ka = 5 - 3(7) = -16
Thus: y = 3x - 16
The relationship between the forms of the line should now be obvious.