Steiner's Theorem, named for Jakob Steiner (1796 - 1863), is included in most high school geometry books but rarely by name. It is often the second in a series of three theorems in a section within the circle chapter. This essay will "start in the middle" and show, with the aid of Geometer's Sketchpad, how the three theorems are related.
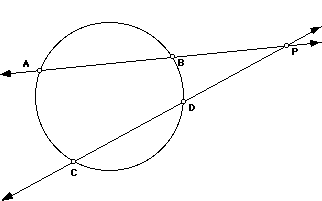
To get the basic figure:
1.) Draw a circle.
2.) Pick a point, P, outside the circle.
3.) Construct any two secants to the circle through P. Mark the
intersections with the circle: A, B, C, and D.

Now, we need to find the relationship represented. The most logical suspicion would be something involving ratios or products.
At this point, the reader may click on stcircle, or whatever is available, to look for the relationship.
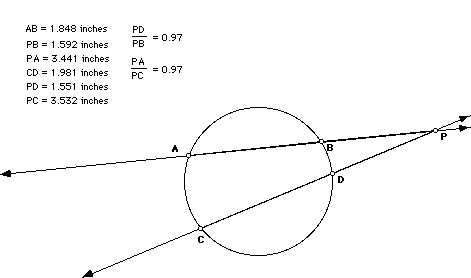
After trying a number of combinations, we discover that
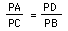 .
.
This of course is the same as (PA)(PB) = (PC)(PD), which is the usual statement of this theorem: i.e. "If two secants intersect in the exterior of a circle, then the product of the length of one secant segment and its external secant segment equal the product of the length of the other secant segment and its external secant segment."
Depending of the experience and level of the reader, it might be sufficient to just see that the previous proportion works for a number of examples. However, to some it may be important to provide a formal proof. For that reason, the following is provided:
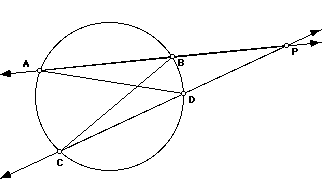
Proof:
For any two points A and B, line segment AB is the set of points
containing A and B, and all points lying between A and B. Thus, we can draw
segments AD and BC to create ADP and CBP. By the corollary which states, if
two inscribed angles intercept the same arc or equal arcs, the angles are
equal, A and C both intercept arc BD, so A = C. The reflexive property allows
P = P. We now have two angles of ADP equal to two angles of CBP, thus by the
AA Postulate, ADP ~ CBP. Since corresponding sides of similar triangles are
proportional we have the final conclusion
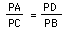 .
.
To visually reinforce this conclusion, move A around the circle and watch as the segments change length, that A remains equal to C, and the ratios remain constant. You may click on "stcircle" above to play with this. One example is shown below.
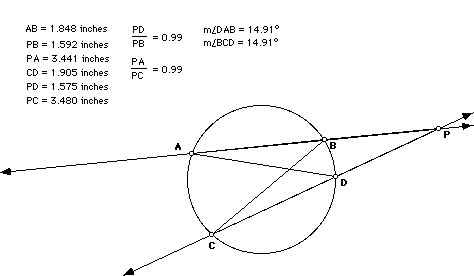
As you move A around the circle, you will hit a point at which AP no longer is a secant, but becomes a tangent to the circle.
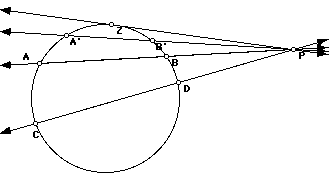
From the above figure, we see that as A moves clockwise around the circle, A and B get closer to each other and coincide at the point of tangency. We call that point Z.
If we check the segment ratios on GSP, we see that our previous
relationship still holds. Since A and B converge at Z, we substitute and obtain
 .
This is the form described by the third theorem in the sequence referred to at
the beginning of this essay. The theorem states: If a tangent and a secant
are drawn to a circle from an outside point, the tangent is the mean
proportional between the secant and its external segment.
.
This is the form described by the third theorem in the sequence referred to at
the beginning of this essay. The theorem states: If a tangent and a secant
are drawn to a circle from an outside point, the tangent is the mean
proportional between the secant and its external segment.
When A is rotated counterclockwise, the secants will intersect inside the circle instead of outside. Thus the secants have become chords.
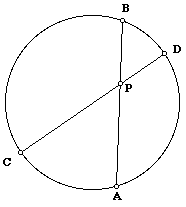
Check the original proportion
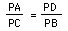 now.
now.
Just as one example: PB = 0.806 inches
PD =0.661 inches
PC = 1.758 inches
PA =1.443 inches
PA/PC = 0.821
PD/PB = 0.821 It still works!
Since we moved P inside the circle, we should give a formal proof for the new figure. It turns out that the steps are almost identical to our first proof.
Proof:
Since there is exactly one line through two points, we can draw segments AC and BD. Using "if two inscribed angles intercept the same arc, the angles are equal," we get A = D because they both intercept arc CB, and C = B because they both intercept arc AD.
APC ~ DPB by AA. Since corresponding sides of similar triangles are
proportional,
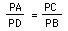 .
This can algebraically be transformed by the means-extremes product to (PA)(PB) =
(PC)(PD), then back to proportion form
.
This can algebraically be transformed by the means-extremes product to (PA)(PB) =
(PC)(PD), then back to proportion form
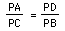 .
.
In summary, we can generalize as follows:
Let two lines, both through P, intersect a circle in points A and B and points C and D respectively. Without loss of generality, let P be in the interior of the circle.
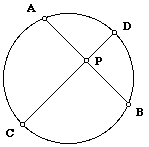
Let P move, on segment AB, toward B. Let AP remain less than or equal to the diameter, while PB approaches 0, i.e. (AP)(PB) approaches 0.
Now consider when P lies on the circle. PB = PD = 0. So
(PA)(PB) = (PC)(PD), thus 0 = 0, and is still true.
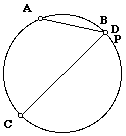
As P moves outside the circle, AP becomes greater than AB. This holds and the theorem remains true as long as the lines through P cut the circle in at least two points.
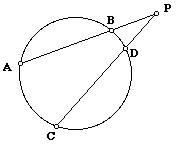
Since we are moving P outward, consider the figure below. When both lines through P are tangent to the circle, we know that the segments AP, BP CP and DP are equal. Does the proportion still hold?
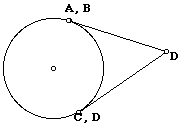
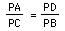
In general, If two lines intersect at point P and intersect a circle at
points A, B, C, D respectively (points are not necessarily distinct) the ratio
that compares the relevant segments is
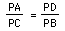 .
.