
Mathematical Essay :: Investigating
Figurate Numbers With Technology
By: Kate Hobgood and Clay Kitchings
What are
Figurate Numbers? Perhaps it might
be helpful to consider various examples that are models for specific figurate
numbers.
For a
detailed method for finding a closed formula for the nth triangular number, use
the link below. The method relies on the use of a TI83/84 calculator (or a
similar calculator with matrix multiplication capabilities):
Pythagoras
is credited to have initially explored the mathematical relationship within
figurate numbers. Pythagoras was a
Greek mathematician and was even titled as “the father of numbers”. He is most well known for the
Pythagorean Theorem, and he “believed that everything was related to
mathematics and that numbers were the ultimate reality and, through
mathematics, everything could be predicted and measured in rhythmic patterns or
cycles”. Mathematicians
would work with the numbers using pebbles or seeds and arranging them into
figures. Working in this manner,
they were able to work with regular polygon numbers noticing a sequence to the
growing figures. Depending on the
number of sides of the polygon and the number of pebbles along a given side, the
figurate numbers were discovered.
Figurate
numbers are numbers that can be represented by a regular geometrical
arrangement or sequence of evenly spaced points. Figurate numbers are most commonly expressed in the form of
regular triangles, squares, pentagons, hexagons, etc. For this reason, figurate numbers are also known as the
polygon numbers. For instance, a
triangle created with three pebbles along a given side results in a total of
six pebbles. Adding one more
pebble to each side of the triangle results in a total of ten pebbles. Therefore, we can find the triangular
sequence of numbers as 1, 3, 6, 10, 15, 21.... *The formulas for figurate numbers will be discussed later
on.* The triangular numbers are
shown in the following figure.

Figure from Wolfram Mathworld.
The
next set of polygonal figurate number that is frequently discussed is called
the square numbers. Similar to the
triangular numbers, each square number is found by the addition of one unit to
two adjacent arms of the square.
Refer to the following figure.

Figure from Wolfram Mathworld.
The figurate numbers correspond to the number of sides of
the polygon. Lengthening two
adjacent sides by one point enlarges the polygon. With each increase, an additional “layer” is added to the
figure. This “layer” is also
referred to as the gnomon. The
gnomon is the piece of the figure that needs to be added to a given figurate
numbers in order to get the next greater figurate number. Gnomons also refer to an architectural
template that is used to mark off similar forms or shapes. The Greek translation of gnomon is “carpenter
square”. For instance, the
formation below represents the sixth square number for there are six units
along a given side. The gnomon can
be visualized as the L-shaped formation of additional units (the figure
contains five gnomons).
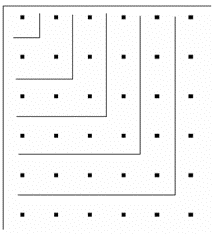
The
gnomon is also related to Pythagoras’ finding of the commonly known Pythagorean
Theorem. Consider the ![]() square created below:
square created below:
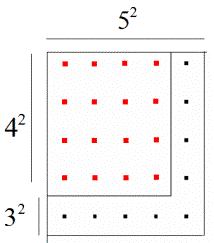
Note
that the backwards L-shaped gnomon or “carpenter’s square” contains nine black
dots, which can be thought of as three groups of three black dots. Therefore, after the total number of
dots in the gnomon, we find that the gnomon can be represented by ![]() dots. Leaving us with a smaller red square
with a width of four dots and a length of four dots. So the smaller red square can be represented by
dots. Leaving us with a smaller red square
with a width of four dots and a length of four dots. So the smaller red square can be represented by ![]() dots. Finally, we know that the entire square figure has a width
of five dots and length of 5 dots.
So here we now have a proof of the Pythagorean triple of
dots. Finally, we know that the entire square figure has a width
of five dots and length of 5 dots.
So here we now have a proof of the Pythagorean triple of ![]() and thus supports the Pythagorean
Theorem for a triangle with two legs of length 3 and 4 and a hypotenuse of 5
units.
and thus supports the Pythagorean
Theorem for a triangle with two legs of length 3 and 4 and a hypotenuse of 5
units.
Notice
that the gnomon of the ![]() figure
is represented by an odd number
figure
is represented by an odd number ![]() . The smaller imagined gnomon of the
. The smaller imagined gnomon of the ![]() smaller
red square (not drawn in the figure) contains seven dots. The even smaller gnomon of a
smaller
red square (not drawn in the figure) contains seven dots. The even smaller gnomon of a ![]() square has five dots. Recall the figure:
square has five dots. Recall the figure:
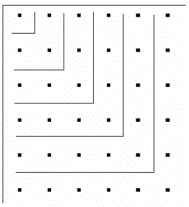
If one
were to continue adding units to the square figure, then the next gnomon of a ![]() square would have 11 dots, a
square would have 11 dots, a ![]() would have 13 dots, and so on. Surprisingly, the sequence of gnomons
can be represented by the odd numbers:
1, 3, 5, 7, 9, 11, 13, 15, 17….
Therefore, with helpful use of the gnomon, one can find support for the conjecture
that the sum of the first n odd numbers is
would have 13 dots, and so on. Surprisingly, the sequence of gnomons
can be represented by the odd numbers:
1, 3, 5, 7, 9, 11, 13, 15, 17….
Therefore, with helpful use of the gnomon, one can find support for the conjecture
that the sum of the first n odd numbers is ![]() .
.

(We think he is a distant cousin,
twice removed).
One
can explore the possible formulas for finding the gnomon of the nth
figurate number. Explore some of
the polygons briefly mentioned above.
The
pentagonal figurate numbers can be expressed as the figure below. The gnomons are shown by the additional
“rings” linking the red dots.

Notice that with each consecutive pentagonal number, one
red dot is added to only two adjacent sides. Since there are two fixed adjacent sides that do not
contribute to the gnomon structure, we have a three-sided gnomon shape. Then, working with the three sides of
the gnomon figure, we can begin summing the gnomon number from the dot placed
on one of the fixed sides. Extend
this ![]() dot to create a side length of n dots. We now have to consider the two sides remaining to complete
the gnomon. The next side will
contain n-1
dots because we do not want to count the dot used on the previous side. The final third side of the gnomon will
also have n-1
dots. Hence, the formula for the
gnomon of a regular pentagonal figure is
dot to create a side length of n dots. We now have to consider the two sides remaining to complete
the gnomon. The next side will
contain n-1
dots because we do not want to count the dot used on the previous side. The final third side of the gnomon will
also have n-1
dots. Hence, the formula for the
gnomon of a regular pentagonal figure is ![]() .
.
The gnomon number for the hexagonal number follows in a
similar manner.

In this case, the gnomon figure is created by four
sides. Working in the same way,
take the ![]() dot on one adjacent side and create a
side length of n
dots. This accounts for one side
of the gnomon, now we must create the remaining three sides. The next three sides will each contain
dot on one adjacent side and create a
side length of n
dots. This accounts for one side
of the gnomon, now we must create the remaining three sides. The next three sides will each contain ![]() dots. The formula for the gnomon of a regular
hexagonal figure is
dots. The formula for the gnomon of a regular
hexagonal figure is ![]() .
.
Notice that the number of sides of the gnomon is found by
(the number of sides of the polygon) – (two adjacent sides) = (n – 2) where n represents the number of sides of
the polygon.
For the square, the gnomon had only two sides. Note that (the number of sides of a
square) – (two adjacent sides) = (4 – 2) = 2.
The gnomon for the pentagon had 5 – 2 = 3 sides.
The gnomon for the hexagon had 6 – 2 = 4 sides.
Since we now know that the gnomon shape has n – 2 sides, and we also know
that one side of the gnomon has exactly n dots, the remaining dots are found on (n – 3) sides. Each of these remaining sides has
(n – 1)
dots.
A more general formula can thus be found for the number of
sides of a gnomon shape for a particular polygon. Letting n be the number of sides of the polygon, we have:
n + (n-3)(n-1)
Extension:
Two-dimensional polygons are not the only figures used to represent the
figurate numbers. They can also be
represented by other shapes such as L-shaped and three dimensional
figures. Expanding the formations
to L-shaped and three-dimensional formations gives rise to a new sequential
relationship. Consider the
pyramidal numbers where each layer of the three-dimensional pyramid has one
less unit along a side length as the layer below it. It may be helpful to picture the pyramidal numbers as a
layering or stacking of the polygonal numbers. This way of thinking is useful when considering any
three-dimensional figure created by regular congruent polygonal faces.