A
Review of Basic Probability: Days 1-2 (or 3)
We’ve
all heard of probability in some shape or form. This is especially true in
election years!
So
what, in its basic form, is probability? What does probability mean?
In
basic terms, probability is
the likelihood that some event
will happen over extended periods of time.
For example, in a standard deck of playing cards
(52 total cards), what is the likelihood
(or probability) that you will choose an Ace
just by choosing one card at random?
Notice the color scheme above. You see, when
determining probability, we are always concerned with some particular “event”
of interest. In the above example,
“choosing a Queen card” would also be an event, but would not be the particular
“event” of interest in the above example.
When determining basic probability, we need to
determine the “sample space” and identify the number of “favorable events.”
![]()
The sample space consists of all the possible
outcomes that could take place. So
in the example of the deck of cards, the sample space would be 52. What would you think “favorable events”
would be for the above example?
So if you pull a card from the deck, we call that a
trial. In simple terms
a trial could be considered any of the following:
Š
Choosing
a card from a deck of cards
Š
Rolling
a number cube
Š
Pulling
a piece of clothing out of your clothes drawer
Š
Flipping
a coin
Š
Testing
a patient in a clinic to see whether or not a new drug is effective
Š
(Perhaps
you get the idea)
There
is another key idea we’ve touched on earlier: the idea of randomness. For example, if you choose a card at random from a 52-card
deck, then you have no idea which card you are going to choose. So the idea of
randomness implies that the outcome of the trial is unknown prior to the trial.
Activity:
If you roll a die (or number cube), what is the probability of obtaining a
1? We’ll use the built-in feature
of the TI-84 “Simulation” Application to determine the long-term results for
rolling a die. We will keep a count of the number of times we see a 1 appear on
the number cube.
In
a moment, you will complete a table like the one below. Let’s suppose that we
roll a number cube 5 times and get the following numbers on the cube after each
trial: 1, 3, 3, 1, 5
We would complete the table as follows:
|
Trial |
1 Occurs? (yes/no) |
Cumulative Proportion of
1’s |
Simplified |
|
1 |
Yes |
1/1 |
1.0 |
|
2 |
No |
1/2 |
0.50 |
|
3 |
No |
1/3 |
0.3333 |
|
4 |
Yes |
2/4 |
0.50 |
|
5 |
No |
2/5 |
0.20 |
In
other words, keep a running total of each one you see. After each trial, divide
the number of ones you’ve seen up to and including that trial and divide by the
number of trials you’ve performed so far.
In the simulation above, we performed 5 trials and had a one appear
twice, so our very last cumulative proportion is 2/5.
The
question remains as to what happens as the trials continue long-term.
Follow
the directions below and complete Table 1.1:
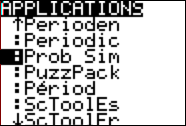
**On
your TI-84, choose the APPS menu:
Choose
“Prob Sim” from the menu:
Then
press any key. If you cannot find “any key,” then the ENTER button will
suffice.
Choose
2, “Roll Dice”.
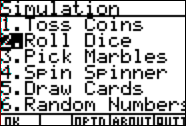
Follow
the instructions on the calculator to count the number of times a 1 is rolled.
|
Trial |
1 Occurs? (yes/no) |
Cumulative Proportion of
1’s |
|
1 |
/1 |
|
|
2 |
/2 |
|
|
3 |
/3 |
|
|
4 |
/4 |
|
|
5 |
/5 |
|
|
6 |
/6 |
|
|
7 |
/7 |
|
|
8 |
/8 |
|
|
9 |
/9 |
|
|
10 |
/10 |
|
|
11 |
/11 |
|
|
12 |
/12 |
|
|
13 |
/13 |
|
|
14 |
/14 |
|
Table 1.1
Questions
for discussion:
1.
In
the “long run” (if you continue the experiment over long periods of time), what
number does the “Cumulative Proportion of 1’s” approach? What if you continue
to roll 50 times instead of 14?
2.
If
you roll a 2 on your first roll, does this determine whether or not you will
roll a 2 on the second roll? (This is the idea of “independence”. In other words, an event
is considered independent if one particular trial does not affect the next
trial. In the example of rolling a die, the result of the first roll will not
affect the result of the second roll.
3.
What
is the overall probability of rolling a tree on one die with one roll?
4.
The
Compliment of an event is defined as all of the other events in the sample
space that are NOT the event A itself. The compliment of A is itself also a
probability. How would you
interpret the idea of the “Compliment of rolling a 1”?
5.
How
would the probability change if we were allowed to count a 1 or a 2 instead of
just the number 1?
Investigation
Two: Passing a True/False Quiz
Suppose
you were given a five-question True/False quiz, but you forgot to study the
night before. You decide, “Hey, I have a 50/50 chance of getting each question
correct.” What does this mean
about your chances of passing the quiz with a perfect score?
How
many possible ways are there to answer a five-question true/false quiz? Let’s create a tree diagram to illustrate the
possibilities after you’ve answered three questions:
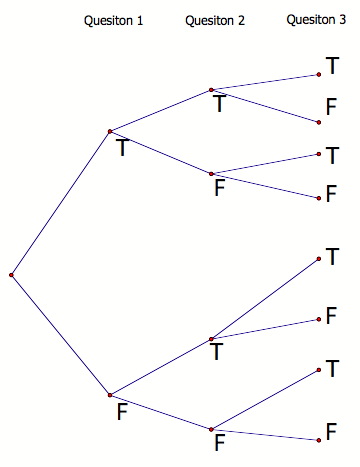
Discussion:
How
many possibilities are there after you’ve answered three questions? Or, to put
it another way, how many different ways could someone possibly answer three
questions? (Hint: how many
“points” are there under the Question 3 column?)
Can
you determine how many ways someone could answer 5 questions on a true/false
test? (Extend the chart if necessary).
If
someone were to randomly guess at each question, what is the probability that
this person will make a perfect score?
Simulation-Extension:
Getting a Perfect Score on a Multiple Choice Test By Guessing Alone
Materials
needed:
*A
Partner
*A
TI83+ or TI84 Calculator (or some other random number generator)
Person
A will take on the role of the “teacher” and will create a 20-question, multiple-choice
(four options) quiz. Using the
TI84 calculator follow the steps below:
From
the MATH button, choose PRB and select option 5:
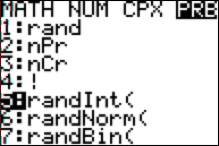
We
wish to generate 20 different answers. For the sake of simplicity, we’ll
generate answers one at a time. We
will call each answer “1, 2, 3, or 4” (just as we would see answers a, b, c, or
d on a multiple-choice test).
Enter “1,4” into the calculator as follows. The calculator will now
generate a random answer, either 1, 2, 3, or 4. Each time you press ENTER, it will
generate another answer for you as the teacher.
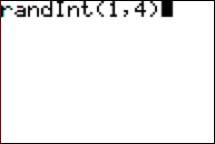
Person
A should perform this calculation by recording the correct answers to the quiz
in the middle column. Continue to press ENTER to generate more random numbers,
1-4. After recording the answers, have your partner guess each answer to each
question without looking. Record his/her answers in the third column and
calculate the score.
|
Question # |
“Correct” Answer (from
the calculator) |
Person B’s answers (by
guessing) |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
Can
you extend your ideas from the true/false quiz to this more extensive quiz?
1.
Explain
how the tree diagram would look different after two questions.
2.
Explain
how the tree diagram would look different after five questions.
3.
How
big is the sample space of possible ways to answer the quiz (with all 20
questions)?
4.
Find
the probability of obtaining a perfect score on this quiz by guessing alone.
5.
Interpret
the idea of “Compliment” of the probability of obtaining a perfect score.
Summarize
what you’ve learned: Create one sentence according to the following conditions:
1.
Use
as many of these words as possible: Probability, Trial, Randomness (or Random),
Independence (or Independent), Sample Space, Event, Compliment, Tree Diagram,
AND
2.
Your
sentence must make grammatical and logical sense.
Teacher
Option: Discuss Venn Diagrams.
A
web applet is available from the following site, which deals with Venn Diagrams
and Probability:
http://stat-www.berkeley.edu/~stark/Java/Html/Venn3.htm
**Click
Here for help from TI concerning the use
of the Probability Simulation APP for the TI84