![MCj04125320000[1]](Drug%20Test%20Activity_files/image001.gif)
Random Drug Testing on the HS Football Team
(Adapted from Statistics: The Art and Science of Learning from by Chris FranklinŐs Statistics. Section 5.4, page 229.)
During the fall of every year, local high school teams battle on the field. The stands are filled with family, friends, and community members who have come to cheer on their team. For the high school boys on the team, the night is full of adrenaline and excitement. Coaches are constantly trying to keep their team positive and healthy. After hearing some rumors going around the school, the coaches gather the football team for a random drug test. Keep in mind that drug usage is illegal and would result in termination from the team.
A urine test is used as an initial screening test because it is the only test within the schoolŐs budget, and it is fairly easy to implement. A few years earlier, the coaches implemented the same drug test and found that the prevalence of drug use was approximately 0.10 (or 10%).
Questions for students:
1. Having a positive test result would result in being kicked off the football team. What is the probability of a positive test result? (Note: use the probability of using drugs or prevalence 0.10 as stated above)
2. Determine the probability of a football player truly using drugs, given that the test was positive.
Working through it:
1. We have been given that the probability of drug use is P(D) = 0.10 where D designates drug user, and Dc represents no presence of drugs.
Sensitivity P(POS|D) = 0.96
Specificity P(NEG|Dc) = 0.93
Here
is a helpful tree diagram: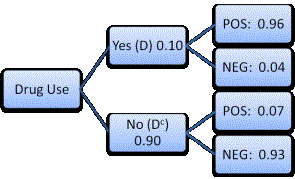
Work through the tree diagram with students to find unknown probabilities.
It may be helpful to use the multiplication rule for intersection probabilities.
To find the probability that the test is positive given that the athlete has taken drugs is:
P(D and POS) = P(POS|D)*P(D) = 0.96 x 0.10 = 0.096
To find the probability that the test is positive when the athlete is truly not taken drugs is:
P(Dc and POS) = P(POS|Dc)*P(Dc) = 0.07 x 0.90 = 0.063
To find the probability that a test is positive, we can add these two probability values together:
P(POS) = P(D and POS) + P(Dc and POS) = 0.096 + 0.063 = 0.159
So there is approximately a 15.9% chance that the test suggests that the athlete used drugs.
OR construct a contingency table:
|
Drugs Present |
POS |
NEG |
Total |
|
Yes (D) |
0.096 |
0.004 |
0.10 |
|
No (Dc) |
0.063 |
0.837 |
0.90 |
|
Total |
0.159 |
0.841 |
1.00 |
2. The probability of drug use, given a positive test is:
P(D|POS) = P(D and POS)/P(POS) = 0.096/0.159 = 0.6038
Therefore, when the drug test shows positive, only about 60% of the time the athlete actually used drugs.
Conclusion:
Since the prevalence rate is close to 0.10, there is a slight chance that an athlete who tests positive for drugs is actually a drug user.
Further Thought:
á Are you surprised at the probability values found in the test? Justify your answer.
á How does this make you feel about some standard drug tests?
á What do you think happened to those athletes who tested positive for drug usage?
References
Agresti, Alan and Franklin, Christine A. (2007). Statistics: The art and science of learning. Upper Saddle River, NJ. Pearson Prentice Hall.