
Problem: Let f(x) = a sin (bx + c) and g(x) = a cos (bx + c). For selected values of a, b, and c, graph and explore:
i. h(x) = f(x) + g(x)
ii. h(x) = f(x) * g(x)
iii. h(x) = f(x) / g(x)
iv. h(x) = f(g(x))
Note: Ordered triples will indicate values for a, b, and c respectively.
Initial Exploration:
First, let us consider the sum of the two functions f(x) + g(x). We will begin with values of (1, 1, 0).
These two versions are often considered the “parent graphs” of both the sine and cosine functions.
f(x) = a sin x
g(x) = a cos x
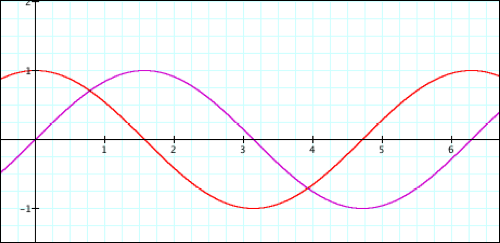
The cycles of the parent graphs are:
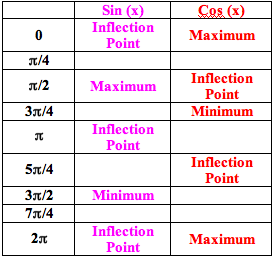
Next, we will define h(x) = f(x) + g(x) with the same values of a, b, and c. The graph is given below.
At first, it seems apparent that the amplitude of h is larger. Why is this? What is its amplitude? Let’s consider what we can determine about maximum and minimum values of h based on what we know about derivatives. We know that there will be critical points where h’(x) = 0. If h’(x) = cos x – sin x and we want to know when h’(x) = 0, this implies that we really want to know where cos x = sin x. Cos x and sin x share values at their intersection points, therefore maximum and minimum values of h(x) must occur where sin x intersects cos x. This is why we see h(x) with a maximum or a minimum each time cos x intersects sin x.
f(x) = a sin x
g(x) = a cos x
h(x) = f(x) + g(x)
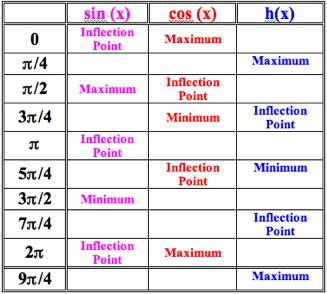
We observe the period of h(x) is unaffected by the periods
of sine and cosine. The period of
h(x) is also 2![]() .
.
The next question we might like to answer is that of the range of h(x); i.e., what is its amplitude?
We already know that ![]() /4
yields the maximum value and 5
/4
yields the maximum value and 5![]() /4
yields the minimum value.
/4
yields the minimum value.
h(![]() /4) =
sin (
/4) =
sin (![]() /4) +
cos (
/4) +
cos (![]() /4) =
/4) = ![]() +
+![]() =
=![]() . Similarly, h(5
. Similarly, h(5![]() /4)
= -
/4)
= - ![]() . We can observe
this informally on our graph of h(x).
Therefore the amplitude is from [-
. We can observe
this informally on our graph of h(x).
Therefore the amplitude is from [- ![]() ,
, ![]() ].
].
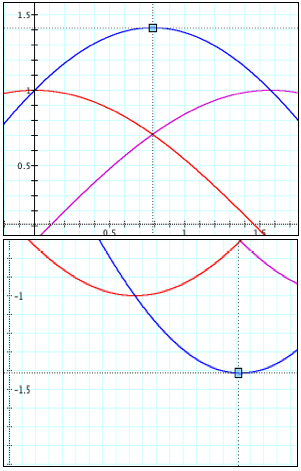
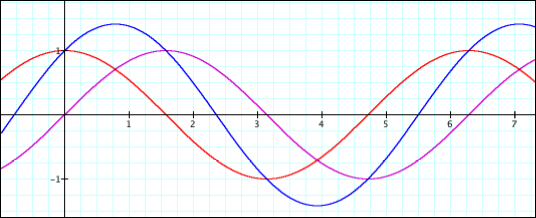
Finally, we will investigate the function h(x) = f (g(x)).
f(g(x)) = sin (cos(x)). First we will consider the graph. g(x) = cos x and h(x) = sin (cos (x)) .
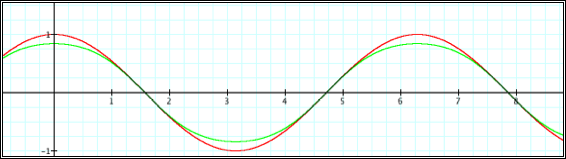
Our first observation is that h(x) and f(x) are quite similar except for amplitude. From observation, we conjecture that it has the same period as well as critical points as cos (x).