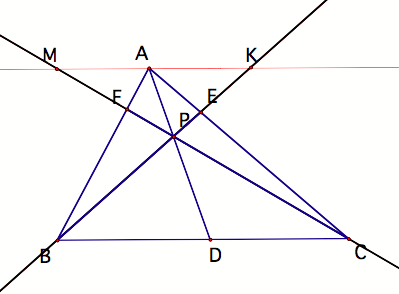
Clay Kitchings :: EMAT 6680 :: Ceva’s Theorem :: Final Write Up Part B

Ceva's Theorem. Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

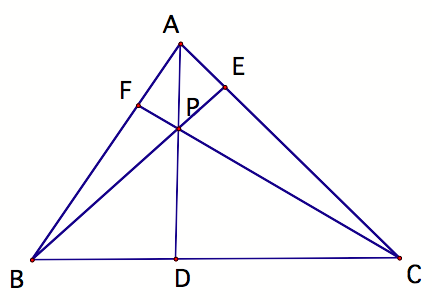
It is worth noting that segments BE, AD, and CF may be referred to as Cevians.

We shall first explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P. 
 According to our investigation with GSP, we find that these two expressions are actually equal for various locations of P inside triangle ABC. Now we shall attempt to verify this conjecture.

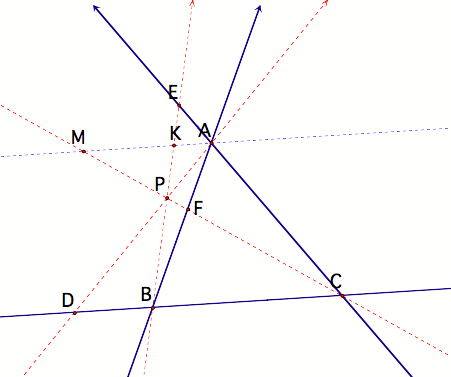
After several attempts at finding similar triangles using auxiliary lines, I finally found some that were helpful. Construct a line (L1) through A that is parallel to segment BC. Extend lines FC and BE so that they intersect L1 at M and K respectively. (To obtain a GSP sketch, click the figure below.)

The alternate interior angles and vertical angles give us AA similarity for numerous pairs of triangles. I shall highlight two of them as examples and then list the others. Triangle KPA is similar to triangle BPD by AA similarity (vertical angles and alternate interior angles).

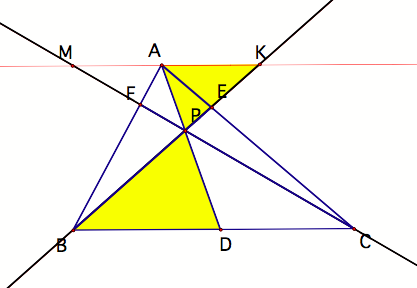
Similarly (pardon the pun), the following triangles are similar:

(a) Triangles MPA and CPB

(b) Triangles KPA and BPD

(c) Triangles MAP and CDP

(d) Triangles KEA and BEC

(e) Triangles CFB and MFA

As a result of the similar triangles, we may now write the following proportions:

1) 2) , 3) , 4)

From the last two proportions, we may write the following proportion (via substitution):

5) è 6)

Now let’s consider these three proportions and manipulate them a little with some algebra:

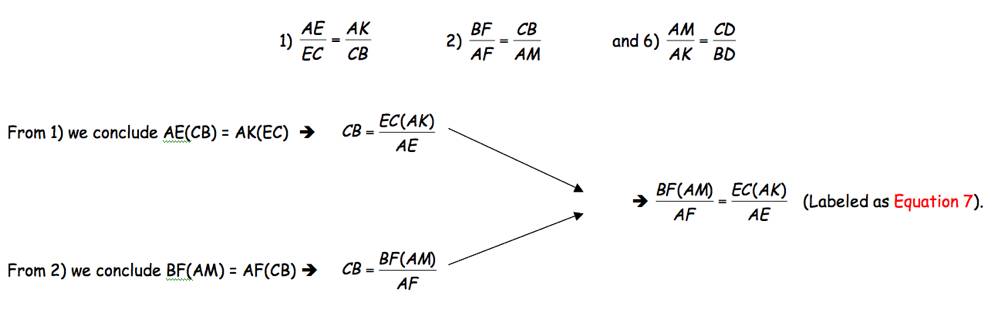
From Equation 7, we may write the following:

EC(AK)(AF) = AE(BF)(AM)

Now, let us divide both sides by AK, simplify, and substitute (using #6 above):

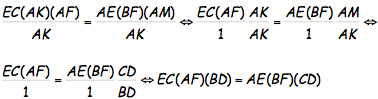
Now we have shown that for segments (Cevians) constructed within a triangle such that they are concurrent, the relationship above holds. Is the converse true? In other words, if cevians of the triangle form the equivalence above, does this imply that the segments are concurrent?

First, we shall assume that in triangle ABC, segments BE and CF intersect at P (on the interior of triangle ABC). Let point D exist such that AF(BD)(CE) = BF(CD)(AE). Now also construct Cevian AD’ through point P.

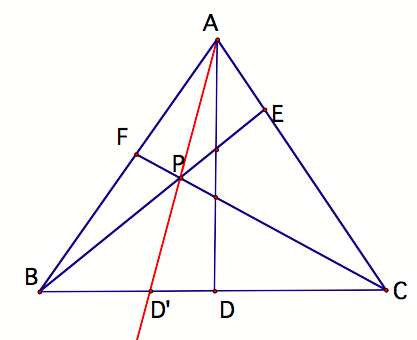
From the previously proved conjecture, we now know AF(BD’)(CE) = BF(CD’)(AE). Now we form the relationship via substitution:

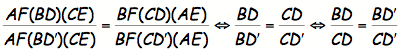
Since the ratio of BD:CD = BD’:CD’, this implies D’=D, which further implies that AD, CF, and BE are concurrent at point P since point P lies on AD’.

Conclusion:

For any triangle ABC, AF(BD)(CE) = BF(CD)(AE) if and only if segments BE, CF, and AD are concurrent.

What if point P is on the exterior of triangle ABC? Click here for a GSP demonstration of this case. A proof for such a case would be comparable to the case with P inside the triangle, and would involve using similar triangles as before.

Ceva’s Theorem allows us to prove points of concurrency for triangle medians, angle bisectors, and altitudes. However, we have to be a bit cautious concerning the intersection of the perpendicular bisectors because they only pass through the vertices of the triangle on special occasions, and thus would not fall under the definition of a Cevian.