
EMAT 6680 :: Clay Kitchings :: Final Write Up ::
Bouncing Barney
Problem:
Bouncing Barney
Barney is in the triangular room shown here. He walks
from a point on BC parallel to AC. When he reaches AB, he turns and walks
parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove
that Barney will eventually return to his starting point. How many times will
Barney reach a wall before returning to his starting point? Explore and discuss
for various starting points on line BC, including points exterior to segment
BC. Discuss and prove any mathematical conjectures you find in the situation.
Preliminary
Drawing: BarneyŐs starting point is point D. We shall assume he completes his
path at a point DŐ, such that![]() .
.
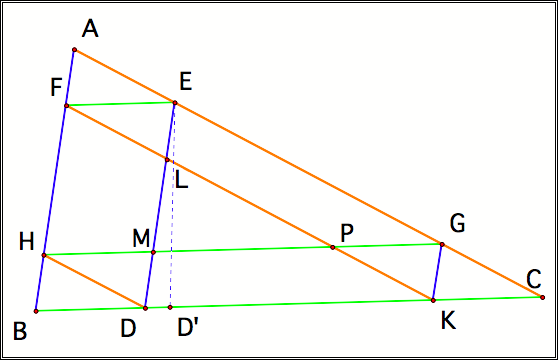
Let
us assume that ![]() ,
which is equivalent in this figure to assuming
,
which is equivalent in this figure to assuming ![]() . We shall also assume that the common,
color-coded paths are parallel (the blue sides will be proven parallel). That
is:
. We shall also assume that the common,
color-coded paths are parallel (the blue sides will be proven parallel). That
is:
HD || FK || AC FE
|| HG || BK
**Note: Any reference to
DŐ shall the assumption that ![]() unless otherwise noted***
unless otherwise noted***
Note #2: It could also be
proven with the assumption that DŐ – D = 0 and showing a contradiction.
Construct
Segment ED. We need to show that
quadrilateral FEDB is a parallelogram because we would like to have FB || ED.
We
have an enormity of similar triangles, some congruent triangles, and some
parallelograms in our figure. We will locate and identify some congruent triangles
and parallelograms.
Let
us start with some parallelograms we already know exist:
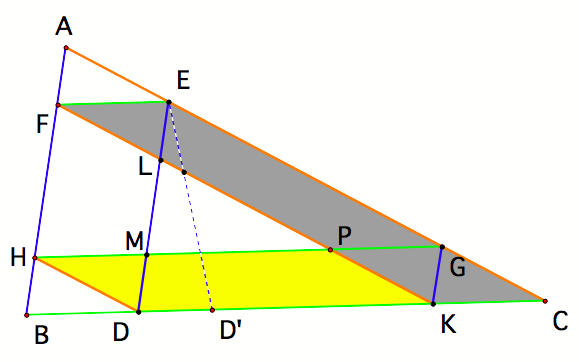
The
following are parallelograms because they have parallel, opposite sides by
definition of BarneyŐs path (two of which are shown above):
FECK, FEGP, PGCK, HGCD, HBKG,
AGKF, and HPKD
From
these parallelograms, we derive the following congruent segments (opposite
sides of a parallelogram are congruent):
FE = PG = KC HD
= PK = GC HB
= GK = AF
We
can now show that ![]() by AAS:
by AAS:
Why?
á
m(BHD)
= m(KGC) and m(HBD) = m(GKC) by the corresponding angles property (due to
parallel lines and transversals)
á
HB
= GK by equality statements above
á
We
have AAS.
We
know triangle FAE ~ triangle BAC by AA similarity
Why?
á
Both
share <A, and m<(AFE) = m<(HBD) by corresponding angles (from the
parallel lines and transversal)
á
This
implies m<(FAE) = m(BHD)
Now
we can write: ![]() .
.
Why?
á
AF
= HB
á
m<(AFE)
= m<(HBD)
á
m<(FAE)
= m(BHD)
á
Use
ASA triangle congruence theorem
Now,
by CPCTC, we have FE = BD, and FE || BD by definition of BarneyŐs path. This implies FEDB is a parallelogram. Why? A quadrilateral is
a parallelogram if it has one pair of opposite sides that are both congruent
and parallel.
Let
us return to the original assumption that DŐ is a distinct point from D. By
assumption, Barney is traveling a parallel path to AB from point E (to point
EDŐ). This implies AEDŐB is also a
parallelogram.
Now,
let us consider our assumption that ![]() .
.
We
know that Barney must travel from point E parallel to AB according to the
definition of his path traveled. Now, we have already verified that FEDB is a
parallelogram. This means that m(FED) = m(FBD), and since FEDŐB is a
parallelogram, m(FEDŐ)=m(FBD) since opposite angles of parallelograms are
congruent. This implies:
**m(FED) – m(FBD) = 0 and m(FEDŐ) – m(FBD) =
0
We
know from angle sums: m(FEDŐ)
= m(FED) + m(DEDŐ)
Now
substitute the highlighted (yellow) parts to obtain:
m(FED) + m(DEDŐ) – m(FBD) = m(FED) – m(FBD) + m(DEDŐ)
= 0
However,
we know from ** that m(FED)
– m(FBD) = 0, and weŐve assumed that m(DEDŐ) > 0. Therefore we now have:
0
+ m(DEDŐ) = 0
This
isnŐt possible because m(DEDŐ) > 0, so we have a contradiction. Therefore
our original assumption that m(DEDŐ) > 0 was invalid. Thus, D=DŐ and Barney
ends his journey exactly where he started it!!!!!