Final

by

Julie Anne Laycock

 

Part 1: Consider the equation xy = ax + by + c

 

 

Let's first look at what happens when we set a and b at 1 and change the c value. In this case, the c is 1,2,3, and 4. We can see we get a set of hyperbolas. As c increases the hyperbolas move up and down the graph by each unit. We can see the x and y intercepts change by one unit as the c changes by one unit.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

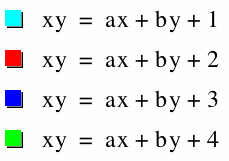
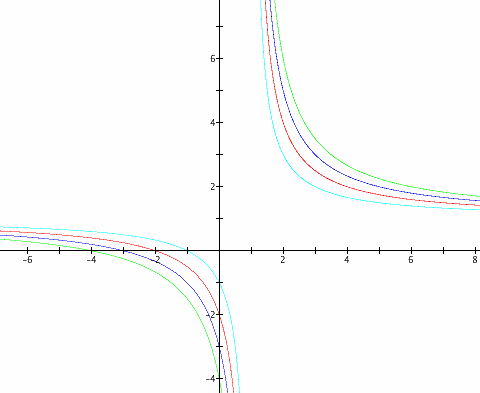
Now let's look at what happens when c is changed to a negative. The c values here are 1, -1, 2, and -2. When the c is -2 we can see the hyperbola has flipped the other direction. And it looks like when c is -1 the hyperbolas connect. Let's look at this a bit closer.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

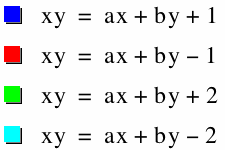
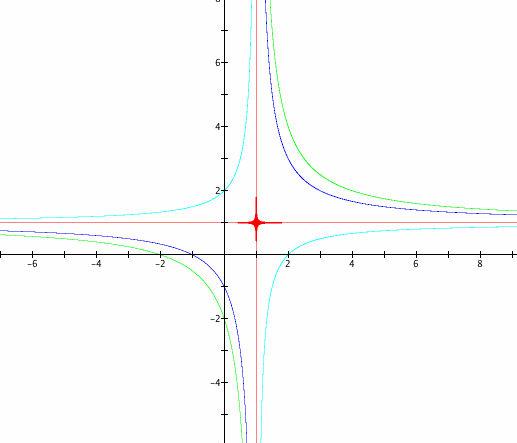
We can see when we set the equations (y - a) and (y - b) equal to zero we get the horizontal and the vertical asymptotes for the hyperbolas. Also when we multiply the equations together and set it equal to n. The animation shows n varying from -5 to 5. We can see that as c gets closer and closer to 0 the hyperbolas are approaching the asymptotes. When c is 0 they hyperbolas merge onto the asymptotes and when c is less than 0 the the hyperbolas flip the other direction. As c gets bigger the hyperbolas move further and further away from the asymptotes. Also, as c gets smaller and smaller the hyperbolas also are moving further and further away from the asymptotes.

 

 

 

 

 

 

 

 

 

 

Part 2: GSP sketch and script tool for constructing a rhombus.

 

Rhombus given an angle and a side.

 

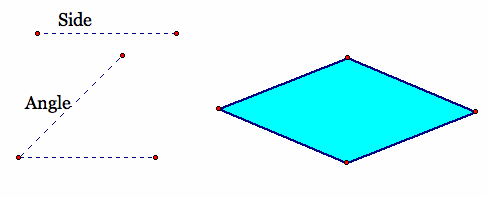
Script tool: Click Here

 

 

 

 

Rhombus given an angle and a diagonal.

 

 

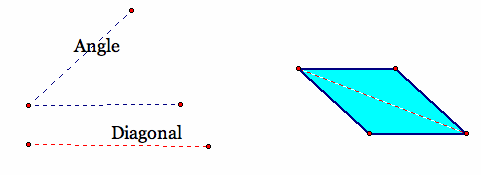
Script tool: Click Here

 

 

Rhombus given an altitude and a diagonal.

 

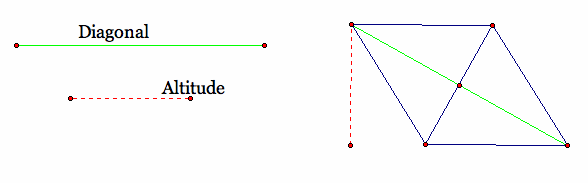
Script tool: Click Here

 

 

 

 

 

 

 

 

Part 3: Write-up of an additional item from the assignments.

 

Explore :

 

 

 

 

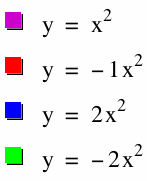
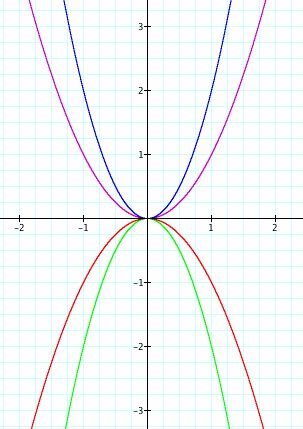
In the graph of we get a parabola with the vertex at the origin. Let's look as what happens to the graph when we change the value of a. In the image on the left a is set at 1, -1, 2, and -2. We can see when the a is positive the parabola is facing up and when a is negative the parabola is facing down. Also, we notice as the absolute value of each number increases the parabola is stretching. Let's look at this a little closer.

 

 

 

 

 

 

 

 

 

 

 

 

 

In this animation the a is varying from 1 to 30. We can see as the the number gets bigger and bigger the parabola is being stretched and it's getting closer and closer to the y axis. Next, let's look as what will make the parabola wider.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

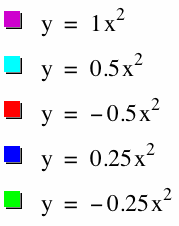
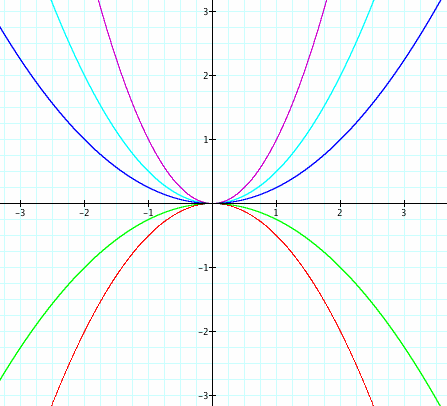
In these graphs, a is set at 1, 0.5, 0.25, -0.25, -0.5. We can see when the absolute value of a gets smaller and closer and closer to 0 the parabola is widening.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

In this animation, the a is varying from 0 to 1. We can see as a gets closer and closer to 0 the parabola is widening until it becomes the x axis when a = 0.

 

 

 

 

 

 

 

 

 

 

 

 

Return