

Exploring Altitudes
by
Julie Anne Laycock
Examine the triangle formed by the points where the extended altitudes meet the circumcircle. How is it related to the Orthic triangle? Will the relationship still hold if the original triangle is obtuse.
First, let's construct a triangle and it's circumcircle.

Remember the circumcircle is constructed by finding the circumcenter which is the point of concurrence of the perpendicular bisectors.
Next, let's construct the altitudes of the triangle.
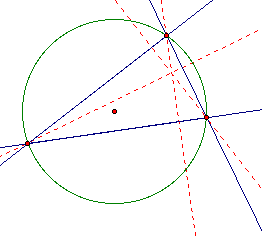
Remember the altitudes are constructed by perpendicular lines from the vertices to the opposite side of the triangle.
Once we have constructed the altitudes of the triangle we can construct two triangles.
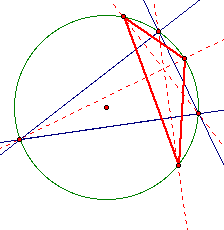
We construct the first triangle by using the intersection of the altitudes and the circumcircle.
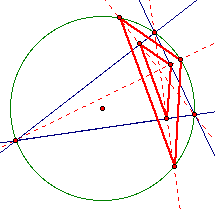
We construct the second triangle by using the feet of the altitudes which is the orthic triangle.
Click Here to manipulate the GSP picture.
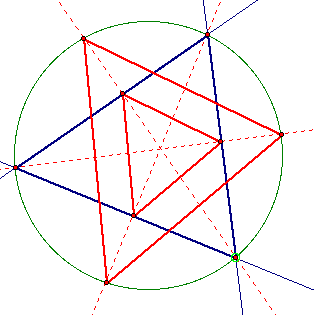
In this case, the big triangles appear to be congruent while the orthic triangle appears to be similar to the other two triangles. Let's look a little closer and move things around to see what is happening.
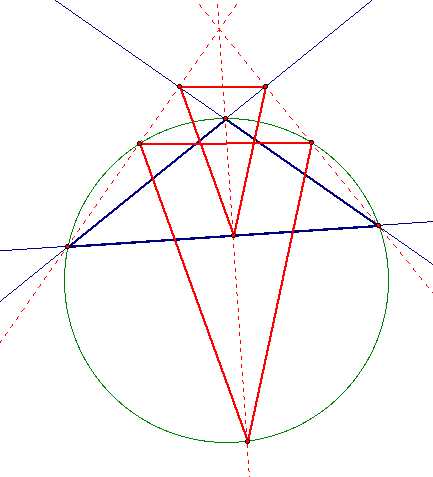
Moving the original triangle we can see the orthic triangle moves outside the circle and the two red triangles still appear to be similar but they don't look congruent or similar to the original triangle.
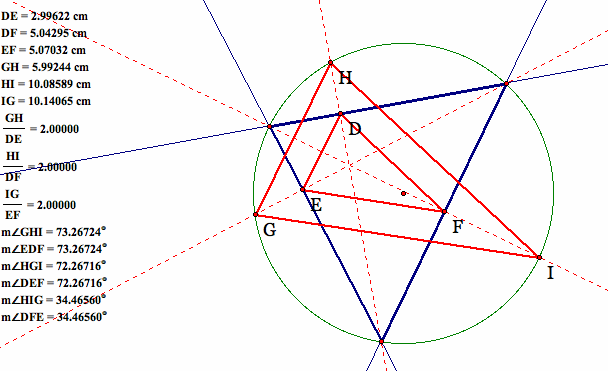
No matter how we move the original circle the two red triangles will be similar. We can see that the proportions of the corresponding sides are all the same and all the corresponding angles are the same so we can confirm that the two triangles are similar by SSS or AAA.
Click Here to manipulate the GSP picture.