

Exploring graphs
by
Julie Anne Laycock
Explore the graphs of: 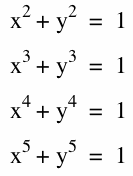
What do we expect of: 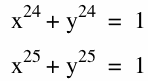
The graph ofis a circle with a radius of 1. The graph crosses the axis at (1,0), (-1,0), (0,1), (0,-1).
The graph of
is a curve that crosses the axis at the point (1,0) and (0,1).
When we put both equations on the graph we can see that the graphs both cross the axis at (1,0) and (0,1) and they also intersect at those points.
The graph of
crosses the axis at the same points as the graph of the circle but the graph is looking more like a square rather than a circle.
The graph of
is a curve that crosses the axis at the same points as the cubed curve but the curve is looking more like the edge of a square.
When we put the two on the same graph we can see that the curve and the square still cross at the same points and they overlap more .
Based on this exploration, I would expect the equations with the even exponents to look more and more like a square and the equations with the odd exponents to look like a curve that would be looking more and more like the side of a square.
I would expect the graph of
to look a lot like a square crossing the axis at (1,0),(-1,0),(0,1),(0,-1). I would expect the graph of
to look like a curve that looks like it could be the edge of a square crossing the axis at (1,0) and (0,1). I would also expect the when putting both on the same axis that the curve overlap the entire side of the square.
We can see the graph of the equations look as we expected.