

Exploring Tangent Circles
by
Julie Anne Laycock
Lets start by creating a script tool for constructing tangent circles.
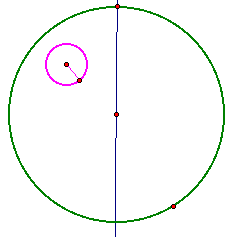
First, construct two circles that are not tangent. Then construct a line through the center of the first circle. Also, construct the radius of the second circle.
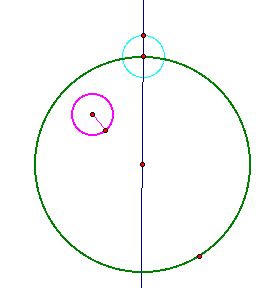
Second, construct a circle with the center on the original circle with the radius of the second circle.
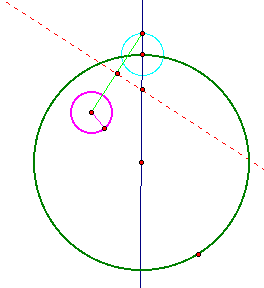
Next, construct a line segment from the center of the second circle to the edge of the new circle. Construct the midpoint of the segment and construct a perpendicular line through the midpoint.
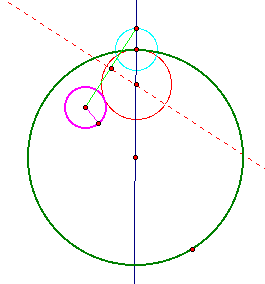
Finally, we can construct the circle tangent to both circles. We us the point where the perpendicular line crosses the line of the original circle and the and the point of the original circle to construct the tangent circle.
To use the script tool: Click Here.
Now we will use this script tool to explore what happens when we move the circles and trace some parts of the circles.
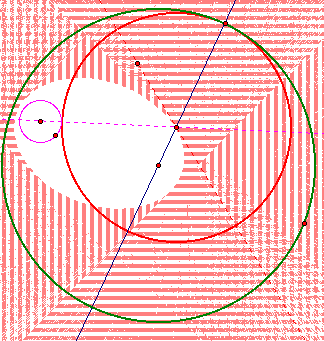
Now, lets look to see what happens when we trace the perpendicular line we constructed. We can see that an ellipse is created. As the perpendicular line follows the tangent circle around the two circles the ellipse is constructed.
Trace the perpendicular line: Click Here.
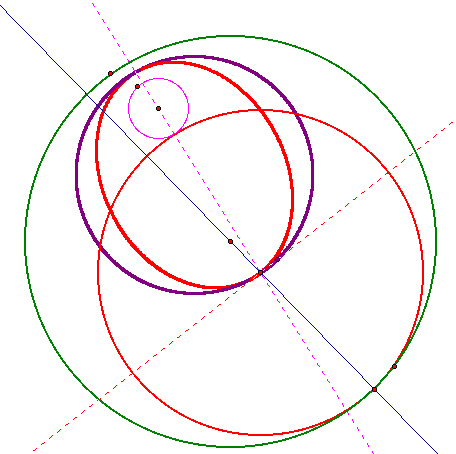
Now lets look at what happens when we trace the center of the tangent line as well as the point on the perpendicular we used to construct the tangent circle. We can see the center of the tangent line constructs an ellipse just like the tracing the perpendicular line but if we look at tracing the point on the perpendicular we see it constructs a circle.
Trace center of the tangent circle and the point on the perpendicular that we constructed to get the tangent circle. Click Here.

Again, let's trace the perpendicular line, but now lets see what happens when the second circle is outside the first circle and the circles are disjoint. We can see that when we trace the perpendicular line we get a hyperbola instead of an ellipse.
Disjoint circles, trace perpendicular lines. Click Here.

Finally, lets look at tracing the center of the tangent line again and the point on the perpendicular line we constructed to get the tangent circle. As we can see we get the hyperbola from the center of the tangent circle but the tracing the point on the perpendicular we get a circle again that is tangent to the hyperbola.
Trace center of tangent circle and the midpoint of the segment. Click Here.