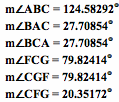Exploring the Original Triangle and its Triangle of Medians
by
Julie Anne Laycock
Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. What relationship do you find between the two triangle?
First, let's start with a triangle and it's medians. Remember the median is the line segment that connects the vertex of a triangle to the midpoint of the opposite side.
Now we need to take the medians and construct a new triangle.
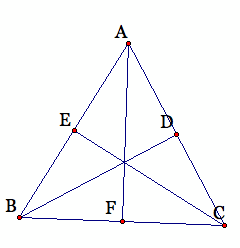
We can see in this case we get an equilateral triangle. Our original triangle was equilateral so it makes sense that the triangle of medians is an equilateral triangle.
For script tool: Click Here
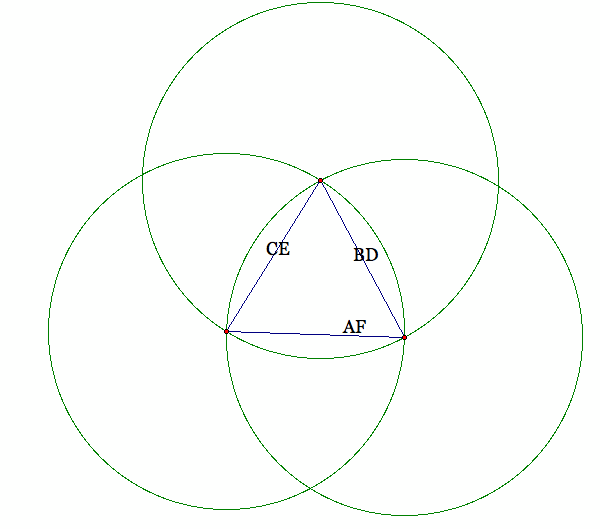
Let's use these figures to explore the relationship of the two triangles.
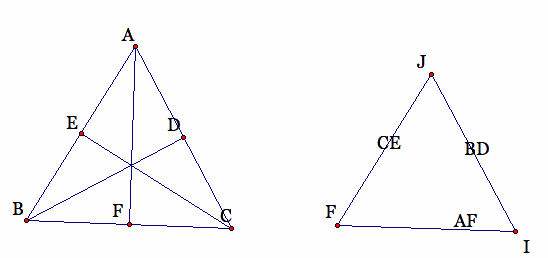
Just by looking at the pictures we can tell both of the triangles are not congruent. However, they are both equilateral and equiangular so they must be congruent.
![]()
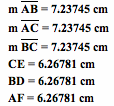
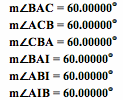
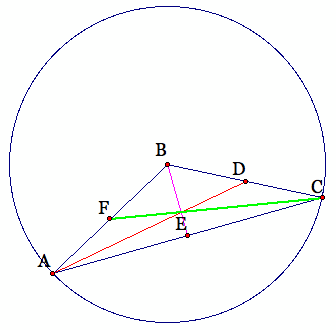
Now, let's look at an isosceles triangle and the triangle of medians.
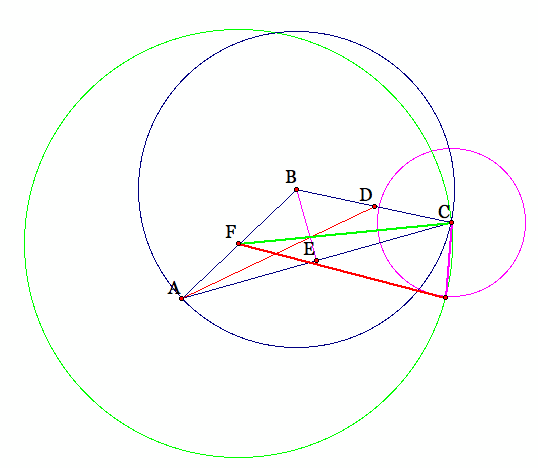
We can see through construction that if we have and isosceles triangle will make an isosceles triangle of medians.
For script tool: Click Here
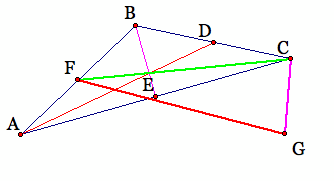
Again, just by looking at the triangles we can see that they are not congruent.
![]()