Centers of Circles
Kasey Nored
This write-up is an exploration
targeted for high school students.
Centroid
A centroid of a triangle is the common intersection of the three medians of the triangle. The median is constructed by finding the midpoint of a side of a triangle and connecting the opposite vertex to the midpoint of the given side.
A centroid will remain inside the triangle for the three types
of triangles categorized by their angles, as shown below.
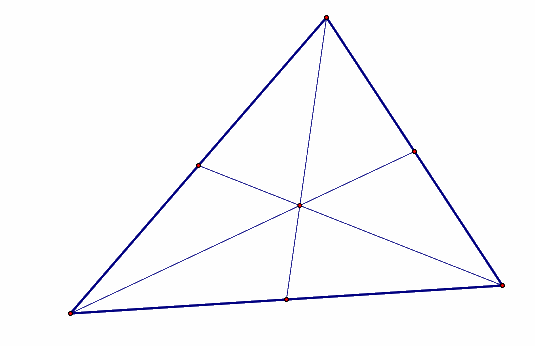Acute Triangle 
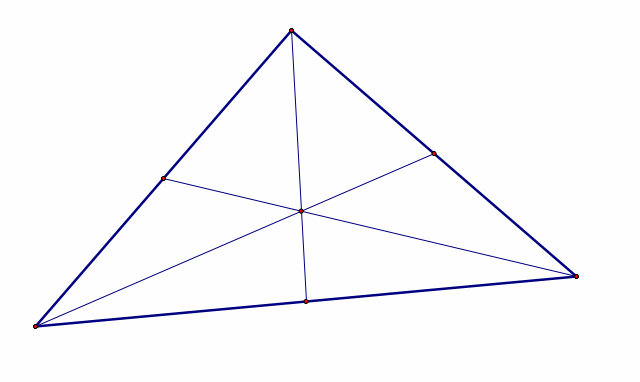Right Triangle
Orthocenter
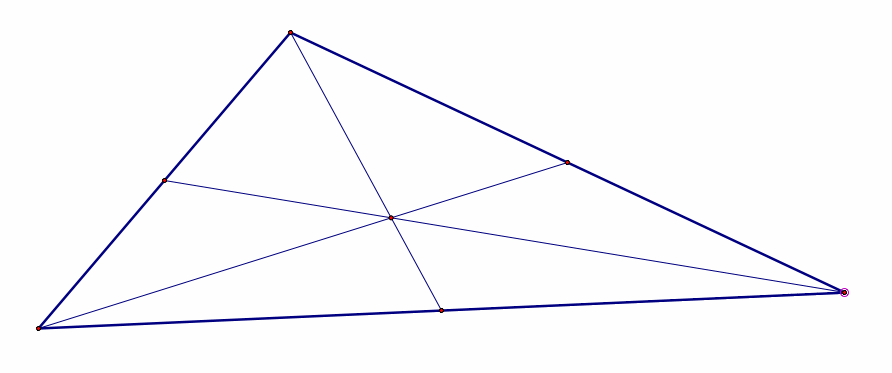
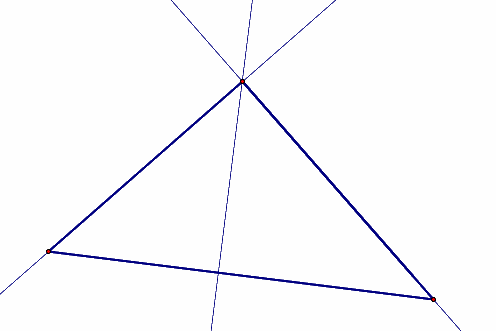
Orthocenters are found by the intersection of the altitudes of a triangle. Altitudes are found by creating a line perpendicular to the line containing the side of the triangle that crosses through the opposite vertex.
Orthocenter
Right Triangle
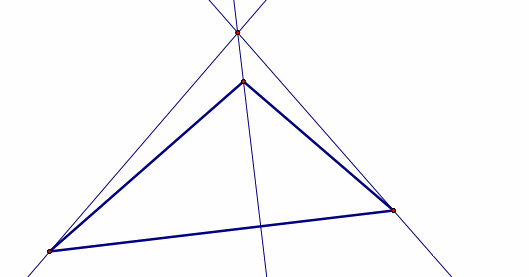Obtuse Triangle
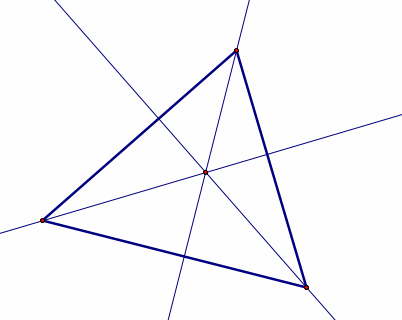Acute Triangle
Orthocenter with Animation What path is followed by the trace of the Orthocenter?
Orthocenter with Traces
Further exploration...
What path does the orthocenter follow when a vertex is animated along a line parallel to the base?
Circumcenter
Circumcenters are found at the intersection of the perpendicular
bisectors of the sides of the triangle.
The perpendicular bisector is created by bisecting
each side of the triangle with a perpendicular line. A circumcenter
is also the center of a circle, which passes through each of the three vertices
of the triangle.
Move any vertex to explore the Circumcenter
Circumcenter
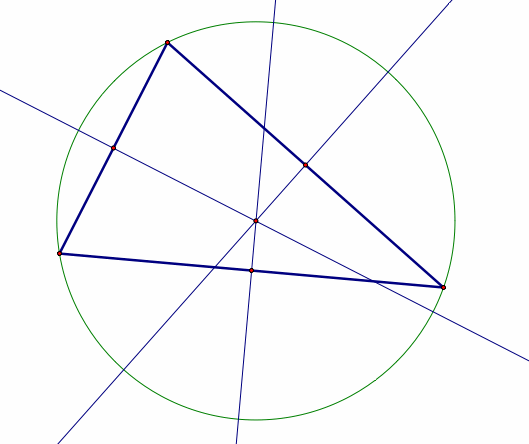
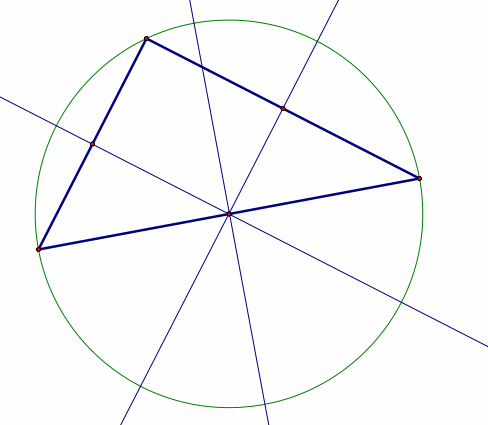
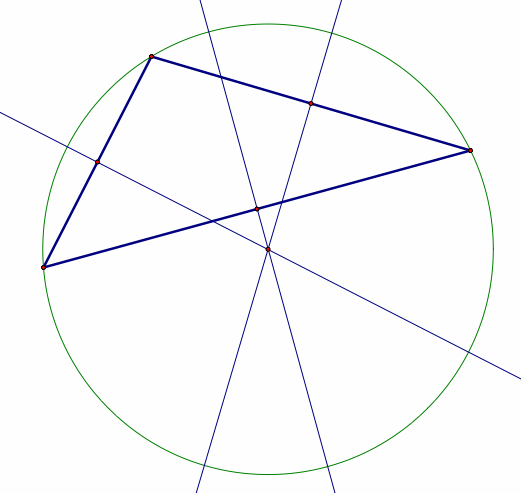Obtuse Triangle
Incenter
An incenter
is found at the intersection of the angle bisectors of a triangle. The incenter
is the center of the incircle, an inscribed circle of
the triangle.
Move a vertex to explore the Incenter. There are some limitations to this construction due to issues with Java and Sketchpad.
This page uses JavaSketchpad, a World-Wide-Web component of The Geometer's Sketchpad. Copyright © 1990-2001 by KCP Technologies, Inc. Licensed only for non-commercial use.
Incenter
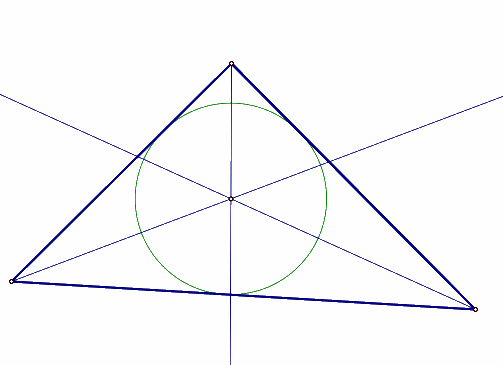
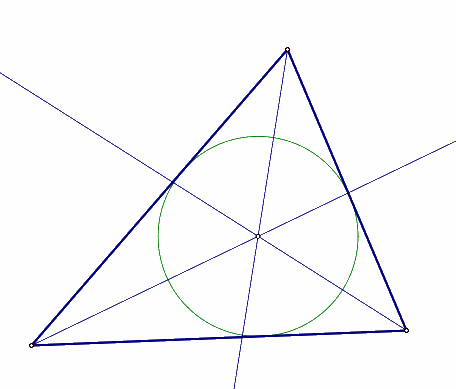
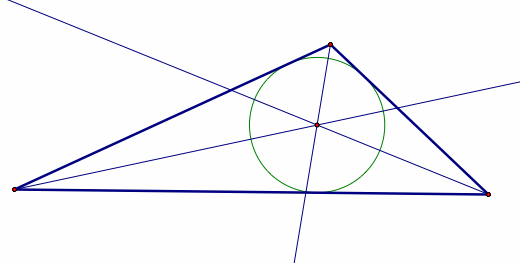
Notice that the intersection of the triangle and the circle only occurs on the angle bisectors for an equilateral triangle. Recall that an equilateral triangle is equiangular also. To find the radius of the incircle drop a perpendicular line from a side to the incenter. This distance is equal from any side.
This page uses JavaSketchpad, a World-Wide-Web component of The Geometer's Sketchpad. Copyright © 1990-2001 by KCP Technologies, Inc. Licensed only for non-commercial use.
Return to EMAT 6680
Return to my page