

Final Assignment: Problem 1
Presented by: Amanda Oudi
Problem 1:
Investigating graphs of the equation xy = ax + by + c
I have decided to use Graphing Calculator to explore the
graphs of the equation. In this investigation, I will keep two variables
constant, vary the other, and note the differences in the graphs.
Example 1: Let a = b
= 1 and let c = 1, 2, 3, 4
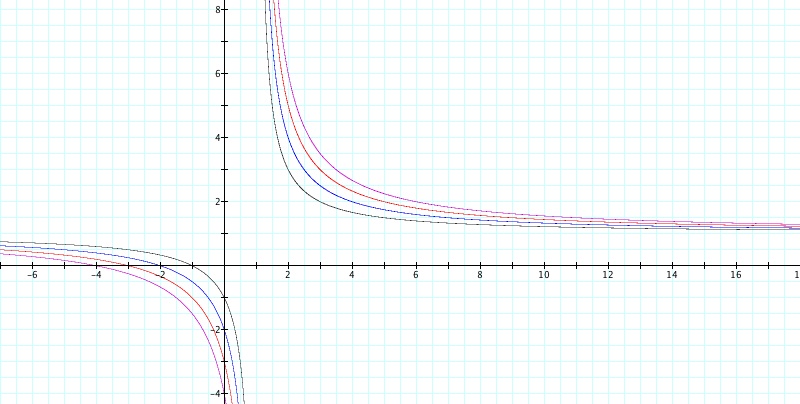
The graphs produced appears to be a hyperbola with asymptotes x = 1 and y = 1. Let’s explore the conjecture graphically by adding the graphs of x = 1 and y = 1.
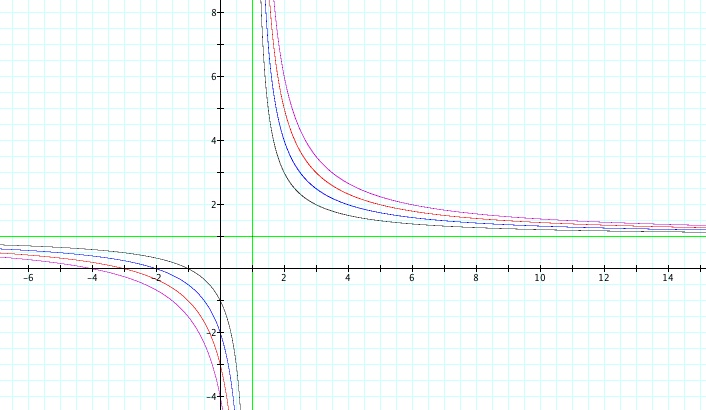
We can solve for the asymptotes algebraically to
determine that the asymptotes are in fact x = 1 and y = 1.
Example 2: Let a = c = 1 and b = 2, 3, 4
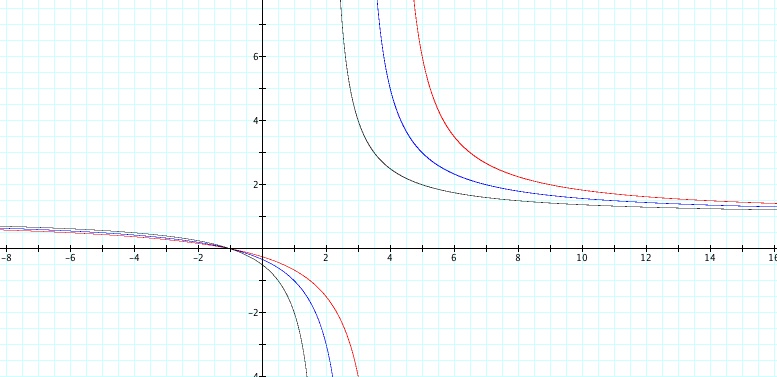
Notice how changing the variable b produces different graphs. It appears that as a and c are constant and b is varied, the vertical asymptotes changes as the variable b changes. The horizonal asymptote appears to remain the same. Also, we can identify the x-intercept graphically and see that it occurs at -1.
Example 3: Let b = c = 1 and a = 2, 3, 4
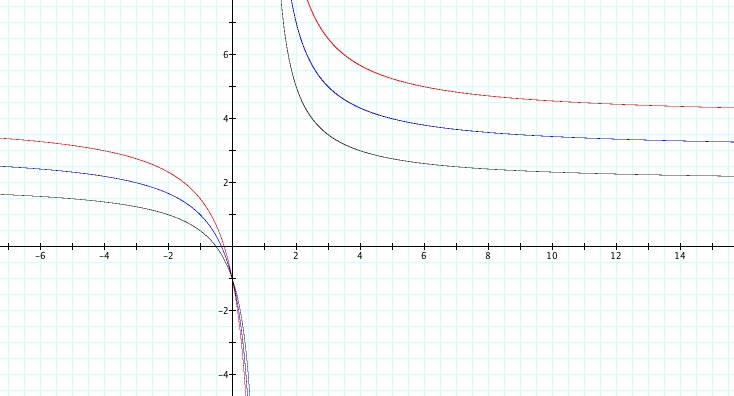
Notice how changing the variable c produces different graphs. In this example, we again obtain different asymptotes. It appears that as b and c are constant and a is varied, the horizontal asymptotes changes as the variable a changes. The vertical asymptote appears to remain the same.
Example 4: Let a = 3 b = 2 and c = 1, 2, 3
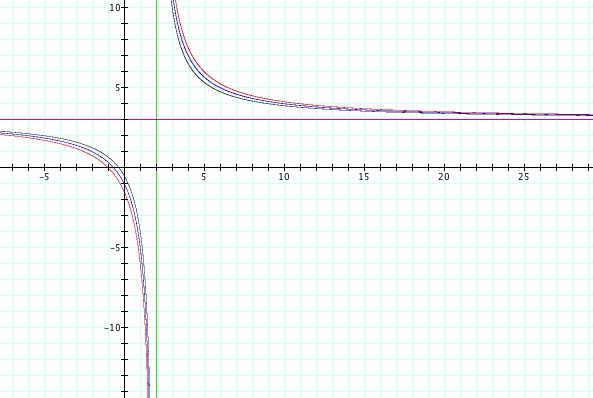
Here, we can identify the asymptotes graphically and claim that the horizontal asymptote is y = 3 and the vertical asymptote is x = 2. Could there be some correlation among the asymptotes and values of a, b? Let's look at a couple other examples.
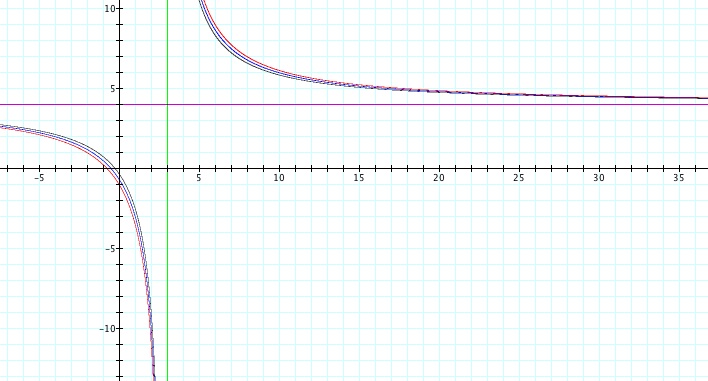
Fig 6: Let a = 4 b = 3 and c = 1, 2, 3
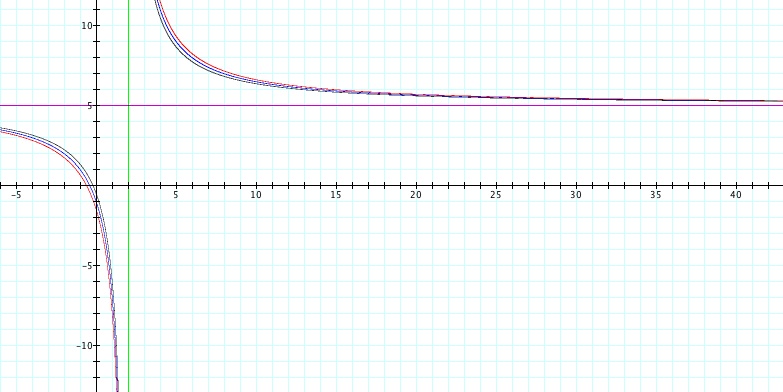
Fig 7: Let a = 5 b = 2 and c = 1, 2, 3
The graphs support my conjecture that as c is varied, the vertical asymptote corresponds to the a-value and the horizontal asymptote corresponds to the b-value.
All the examples explored use positive values for a, b, c. What is one of the values were negative? How might that change the graph of the hyperbola? I'll leave that up to the reader as an extension.