Assignment 2: Quadratics

Presented by: Amanda Oudi

Problem: Graph the parabola y = 2x² + 3x – 4

i.       Overly a new graph replace each x by (x – 4)

ii.     Change the equation to move the vertex of the graph into the second quadrant

iii.   Change the equation to produce a graph concave down that shares the same vertex

iv.   Generalize

Discussion:

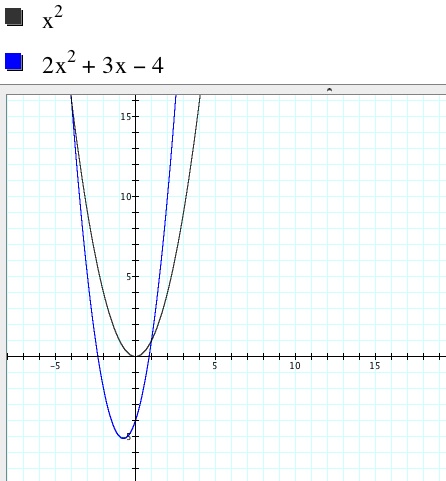
Recall the general form of a quadratic: ax² + bx + c. Let’s begin by first graphing the given parabola. We see that the parabola opens upward. Its vertex is not at the origin like its parent function x². The vertex of this parabola lies in the third quadrant and is the minimum point on the parabola. The parabola is also shifted horizontally to the left by n units.

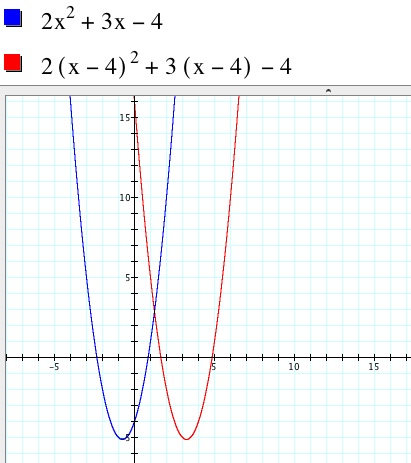
Case i. Now replace each x by (x – 4). We see that the graph has shifted 4 units to the right.  Why is this? Recall vertex form of a quadratic: (x – h)² + k (we will assume our readers understand the derivation of this form using the concept of completing the square). The equation after substitution yields y = 2(x – 4)² + 3(x – 4) – 4. So the graph shifts 4 units to the right since 4 is a positive integer.

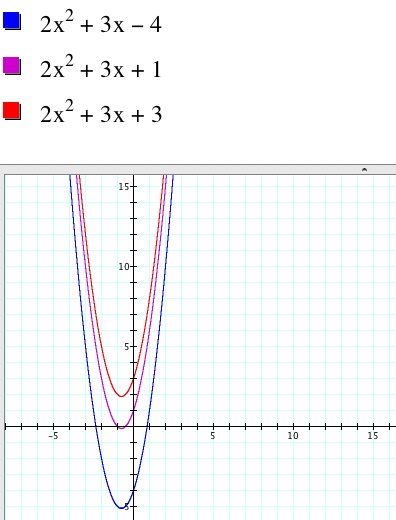
Case ii.

Now we wish to move the vertex so that it lies in the second quadrant. How might we achieve this? From Case i, we saw that a positive integer shifted the parabola horizontally towards the right. So we can guess that a negative integer will shifted the parabola horizontally towards the left. In this case, we are looking for a vertical shift rather than a horizontal one. We see that the vertex of our original equation has a y-value of about 5. So we need to change the equation so that our graph shifts at least 5 units up. If we change the c-value in the equation y = 2x² + 3x – 4, then we will obtain the desired graph.

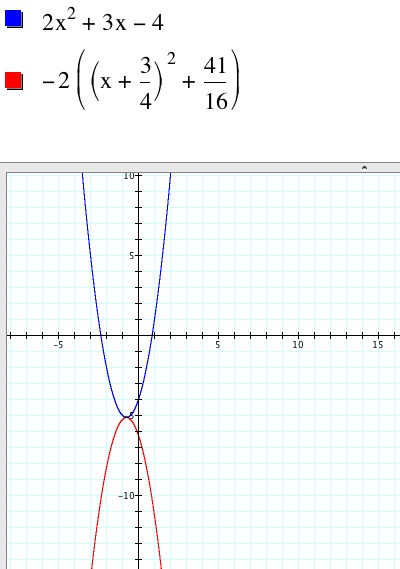
Case iii.

Now we want to change the equation so that our graph is concave down. Let’s first try by making the leading coefficient a negative one. The resulting graph is one that is concave down, but it does not share the same vertex. Instead, let’s determine the vertex by using the method of completing the square, thus allowing us to write y = 2x² + 3x – 4 into standard form.

Completing the square gives:

y = 2x² + 3x – 4

   = 2(x² + ³/₂x – 2)

   = 2[(x² + ³/₂x + ⁹/₁₆ – 2 – ⁹/₁₆)]

   = 2[(x + ³/₄)² – ⁴¹/₁₆]

Recall standard form of a quadratic: (x – h)² + k, where (h,k) indicates the vertex. So, the vertex is (-³/₄, -⁴¹/₈)

Extension: Can you determine another method of determining the vertex?

Continuing on, we know that if a < 0 (i.e. leading coefficient is negative) then the parabola will be concave down. We also have to keep in mind that we want the same vertex as before, so we must change the sign of the k-value in the equation of well. Doing so gives us: y = -2[(x + ³/₄)² + ⁴¹/₁₆].

Case iv.

So what can we conclude as a result of this investigation? We noticed that we can shift the graph horizontally left or right by replacing x with (x + a) or (x – a). We also noticed that we can shift the graph vertically up or down by adding a constant at the end of the equation.  Lastly, we looked at determining the vertex of the parabola and how might we change a parabola from concave up to concave down. We found that a simply way of determining the vertex is by putting the given equation into standard form using the method of completing the square, and then to change the direction in which the parabola opens, we change the sign of the leading coefficient (i.e. sign of the x² term).