Assignment 3: More about Quadratics

Presented by: Amanda Oudi

Problem: Investigate graphs in the xb plane

Discussion:

Consider the equation x² + bx + 1 = 0.

Now graph this relation in the xb plane. In order to do so, we must solve for the variable b in the given equation. Doing so gives:

x² + 1 = -bx

- (x² + 1) / x = b

So now we can graph the relation in the xb plane using Graphing Calculator.

Now suppose we take any particular value of b, say b = 6, and overlay this equation on the graph. We see that it results in a line parallel to the x-axis. In particular, if b = 6 intersects the curve in the xb plane, the intersection of points correspond to the roots of the original equation for that value of b.

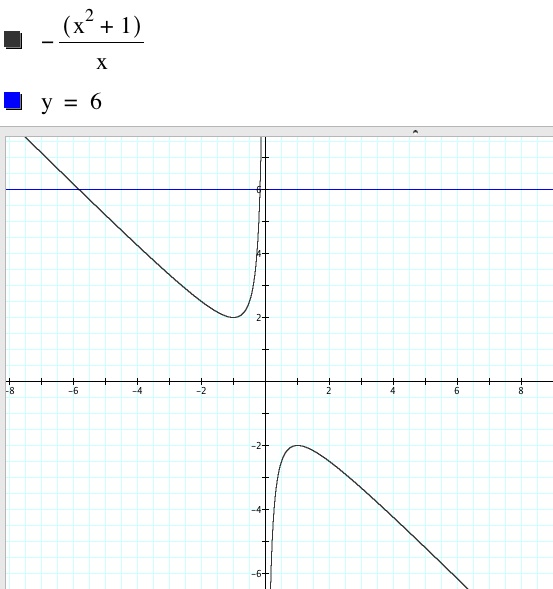
We see that the line b = 6 intersects the graph in two places. Both intersections occur in the second quadrant, thus indicating that two roots exist and both are negative values.

We can determine the roots of the parabola for y = x² + 5x + 1 for b = 5 on the xy plane by using the quadratic formula. Doing so gives:

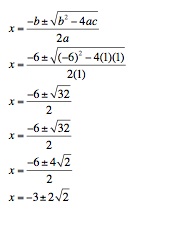
The decimal approximations of the roots are x = - 0.17 and x = - 5.83. We can trace the graph given the xb plane using Graphing Calculator to observe that the intersection is are the same x-values that we computed from the quadratic formula that corresponded to the equation in the xy plane. So we can propose that the x-value of the intersections of the line b = n and y = x² + bx + 1 on the xb plane will yield the same x-values as the equation in the xy plane.

Now consider several lines of b = n.

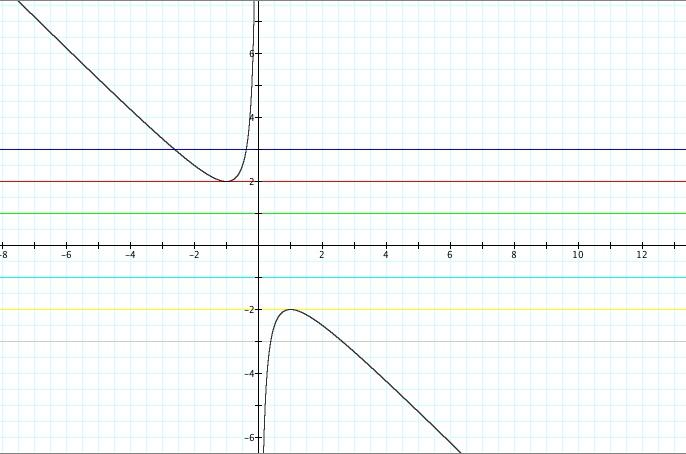
We see that b > 2, two negative real roots occur. When b = 2, there is exactly one negative real root. When b < -2, there are two positive real roots. Lastly, when b = -2, there is exactly one positive real root. Why is this the case? Consider what is happening to the discriminant in the quadrant equation when a = c = 1. If b > 2, then the discriminant will be b² – 4, which will always result in a positive number, and the square root of a positive number will yield a real number. When we complete the computation of the quadratic formula, we obtain two negative real roots when b > 2. Similarly, if b < -2, then the discriminant will be positive, and the completed computation of the quadratic formula will yield two positive real roots. If b = 2 or -2, then the discriminant will be 2²  - 4(1)(1) = 0 or (-2)² – 4(1)(1) = 0 Since the square root of 0 is 0, we will always get one real root. If – 2 < b < 2, no real roots occur because the line b = n never intersects our graph of x² + bx + 1.

Now consider the case when c = -1

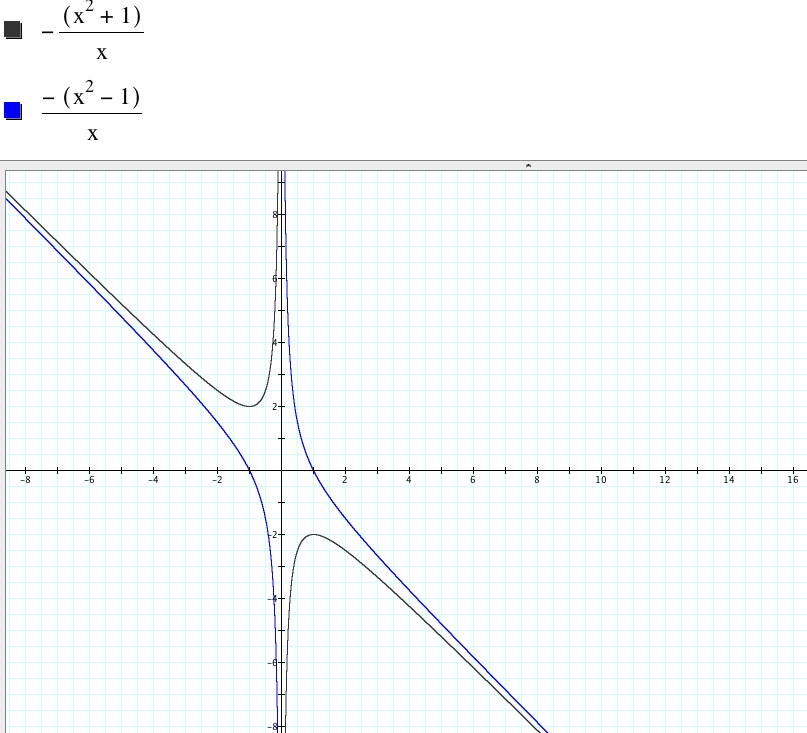
Now if we visualize b = n, we can picture the horizontal line crossing the graph again at two points, thus indicating that two real roots exist just as before when c = 1. This makes sense because the discriminant with c = -1 is b² – 4(1)(-1) = b² + 4, which will always yield a positive value. Hence, two real roots will occur and these roots are x = -1 and x = 1. We can verify this algebriacally or graphically.

Let's investigate what happens when we change the value of c. What happens when c < 0?

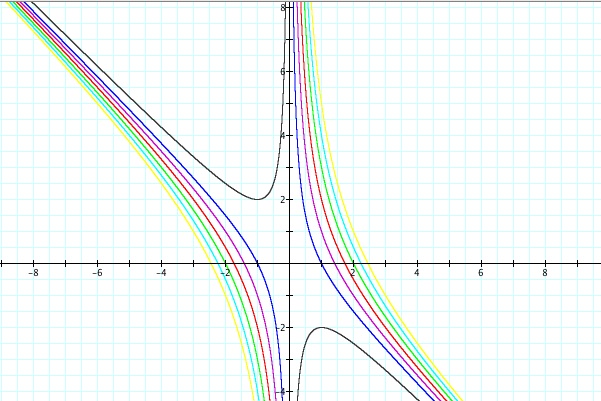
So we see that when c < 0, for any b = n, two real roots occur. What about when c = 0?

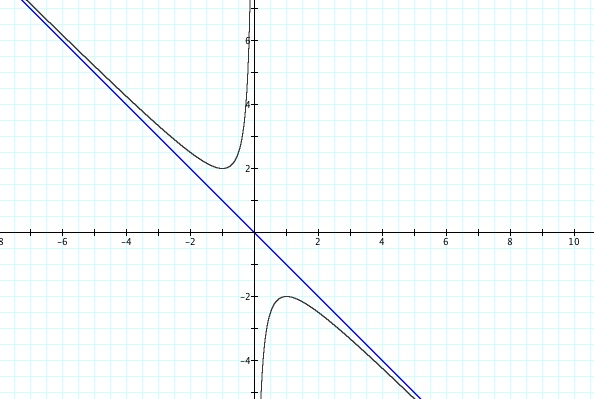
When c = 0, we see that the graph is that of a a linear function. Thus, for any b = n, only one real root occurs, as seen below.

What happens when c > 0?

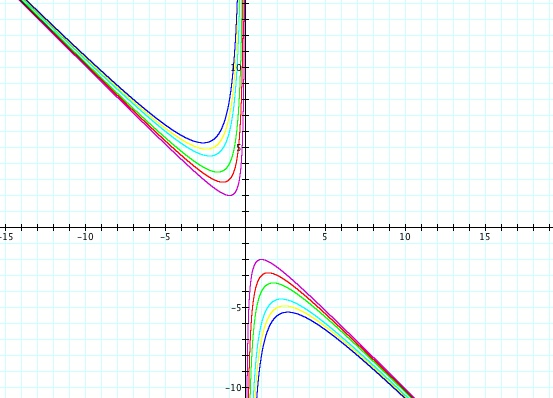
When c > 0, for any b = n, the number of roots depends on the value of b. Depending on b, we may have two real roots or at some values of b we will have no real roots.

Return to Main Page