Assignment 6: Explorations with Geometer's SketchPad
Presented by: Amanda Oudi
Problem: Given three points A, B, and C, draw a line intersecting AC in the point X and BC in the point Y such that AX = XY = YB.
Discussion:
We are given three noncollinear points A, B, C. Let's connect points A and C to form segment AC and connect points B and C to form segment BC.
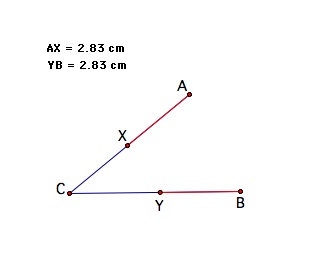
Now we want to find points X on AC and Y on BC such that AX = XY = YB. We can begin by plotting points X on AC and Y on BC just to get an idea of what we want to accomplish.
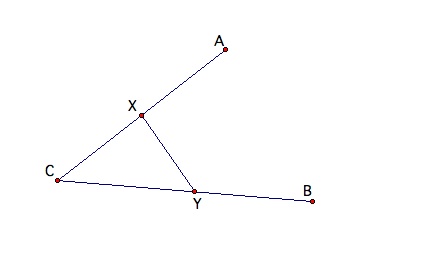
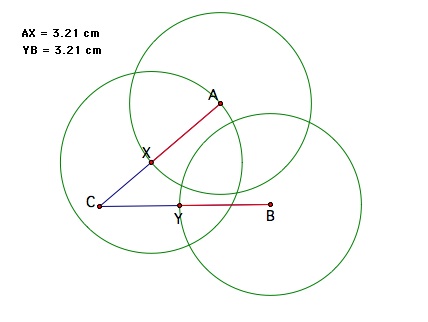
My idea here is to construct circles with centers A and B, such that these two circles share the same radius. So, I began with constructing a circle with center A and arbitrary radius (to choose an arbitrary radius, I placed an arbitrary point on segment AC and called this point X and then let AX be my arbitrary radius). Then, I constructed a circle with center B and the same radius (= AX) as the previous circle. Label the intersection of the newly constructed circle and segment BC point Y. Now we have created AX = YB. It is easy to see this is the case because as you move point A, AX and BY remain lengths of equal measure.
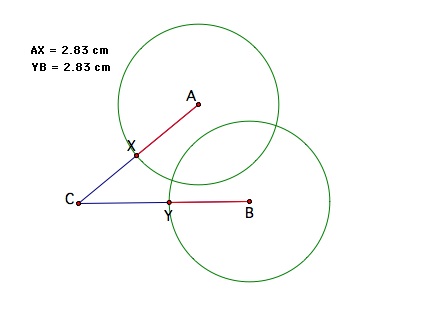
Now let's construct a circle centered at X with radius AX.
So far we have shown that AX = YB. What's left to show is that AX = YB = XY. We can take center X and move the point so that the circle formed by this center and radius AX intersects point Y. Doing so now indicates that the circle has center X and radius XY. Thus, AX = YB = XY holds at this point.
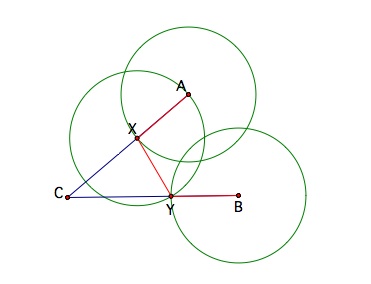
Therefore, we have found points X and Y such that AX = XY = YB.
Now, I was able to determine the location of points X and Y through the use of Geometer's SketchPad. Because of the dynamic and interactive interface of the software, I was able to move the points around in such a way that satisfied the relationship. What if I had paper and pencil rather than Geometer's SketchPad? So, let me discuss another solution that does not rely on the movement of points.
Begin by plotting point X' on AC. Then construct a circle with center X' and radius AX. Likewise, construct a circle with center B and radius AX. Label the intersection of this circle with BC as Y'. So, AX' = Y'B because the segments are radii of congruent circles.
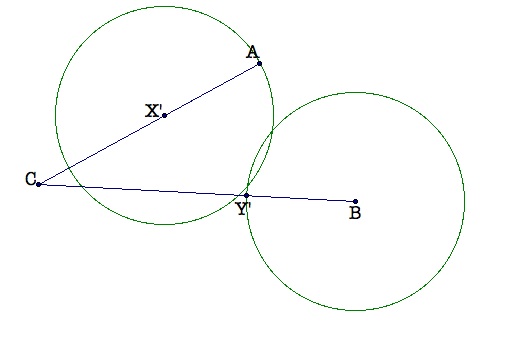
Now connect AB. Construct a parallel line to AB through Y'. Label the intersection (the one that occurs inside of ACB) of this parallel line with the circle with center X as Y''.
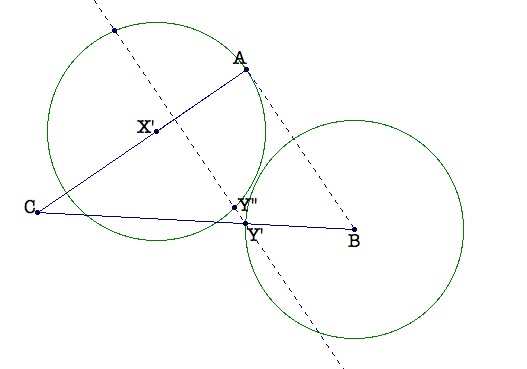
Now construct a parallel line to CB through X'. Label the intersection of this parallel line and AB as B'. Then, form quadrilateral X'AB'Y''.
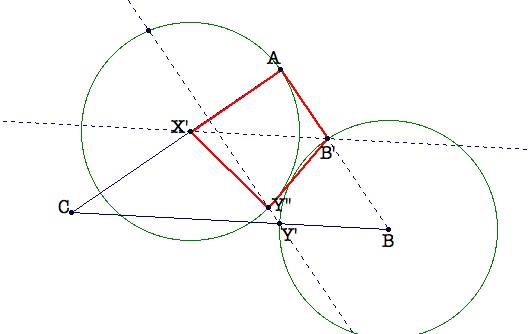
Now, let's project Y'' onto CB to locate Y. Then, construct a parallel line to X'Y'' through Y. The intersection of this line with AC locates X.
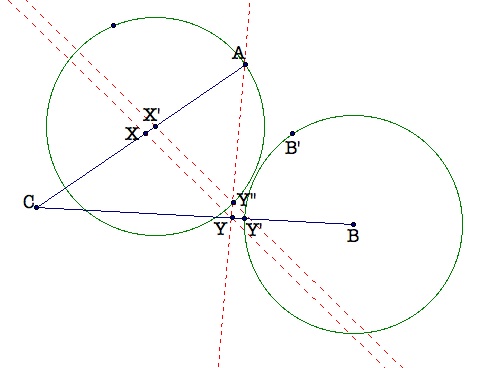
Now we have found three equal segments: AX = XY =YB.