Assignment 7: Tangent Circles

Presented by: Amanda Oudi

Investigation: Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.

Discussion:

I will begin by discussing the construction of a circle tangent to two circles using GSP in a step-by-step manner.

1.     Using the circle tool, create a circle with center A

2.     Using the circle tool, create another circle with center B. Draw this circle so that is lies inside circle A

3.     Draw a line that passes through the center of circle A and a point C on the circumference of the circle.

4.     Now we want to construct a circle with center C that is congruent to circle B. Do so by constructing a circle with center C with radius of circle B

5.     Label the intersection of AC with circle C point D (we will label D as the intersection point that lies outside of circle A)

6.     Construct segment BD by joining point D and the center of circle B

7.     Find the midpoint of BD and construct a perpendicular line to BD passing through the midpoint

8.     Label the intersection of the perpendicular line with AC point E

9.     Point E is now the center of the tangent circle

10.  Construct the tangent circle with center E and radius EC

A snapshot of the resulting construction:

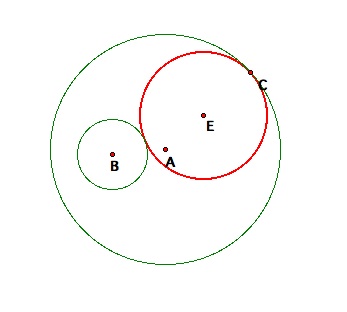
Here, we see that circle E is tangent to our two given circles, circle A and circle B, and point C is the one point of tangency.

In this case, we have created a circle tangent to two other circles, where one circle is inside the other. Exploring this GSP Sketch, we can animate point C around circle A and trace center E. Doing so creates the light blue ellipse. It looks like the foci of the ellipse is located at the center of circle A and center of circle B.

Now, I will create a script tool for the construction of tangent circles, that way we can easily explore the case when the two given circles intersect and when the circles are disjoint. Using the tangent circle script tool, we notice that when the circles intersect the trace seems to form an ellipse and when the circles are disjoint the trace seems to form a hyperbola.

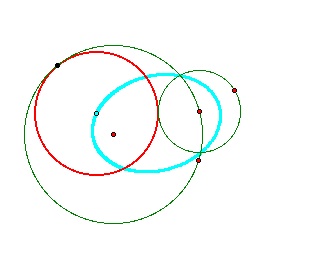
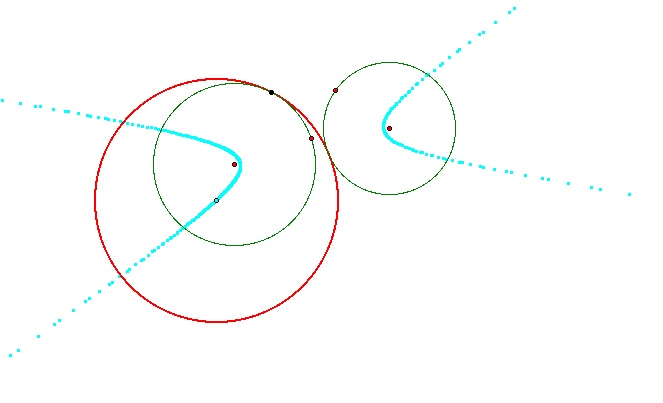
This investigation was an interesting one because my knowledge about tangent circles is rather limited. I learned about tangent circles (construction of them) in Math 5200, but never investigated the trace of the center or the loci, so I found that this was a good exploration that utilized GSP.

Return to Main Page