

Assignment 8: Altitudes and Orthocenters
Presented by: Amanda Oudi
Orthocenter of triangle ABC:
As the shape of the triangle
varied, the location of the orthocenter changed. For an acute triangle, the
orthocenter is within the triangle. For an obtuse triangle, the orthocenter
lies outside the triangle because the altitude and sides of the triangle must
be extended thus causing the intersection to lie outside the triangle. For a
right triangle, the orthocenter is on the vertex of the right angle.
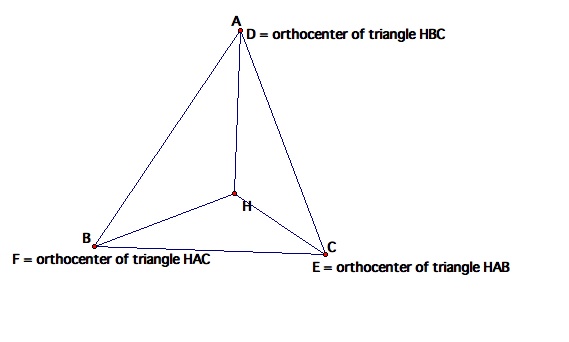
What was interesting was the
location of the orthocenter of the sub-triangles of ABC. The orthocenters of
the sub-triangles always remained on one of the vertices of triangle ABC. I was
not expecting this to happen, for I thought the orthocenters would be somewhere
within the sub-triangles. Explore the orthocenters using this GSP sketch.
Conjecture:
The orthocenter of each sub-triangle
is located on a vertex of triangle ABC.
Proof:
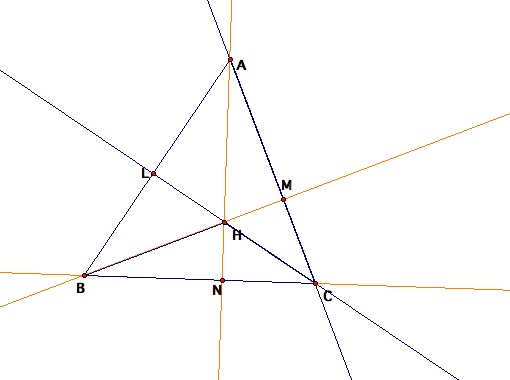
Begin by constructing the
altitudes of triangle ABC. We see that the line containing the altitude from
vertex A and perpendicular to BC forms a right angle at N. Likewise, the line
containing the altitude from vertex B and perpendicular to AC forms a right
angle at M. Again, the line containing the altitude from vertex C and
perpendicular to AB forms a right angle at L. The intersection of the altitudes
is the orthocenter of the triangle.
Consider triangle AHB. To determine the orthocenter of this triangle, we must construct the altitudes from each vertex. We see that points C, H, L are collinear. So the line CL is perpendicular to AB. This side is common to both triangles AHB and ABC. Therefore, the altitude from vertex H and perpendicular to AB is HL has already been formed since it is contained in the line CL. Now consider the altitude from vertex A and perpendicular to HB. The altitude is AC. Now, consider the altitude from vertex B and perpendicular to HA. The altitude is BC. So, the three lines containing the altitudes are CL, BC, and AC. All three lines intersect at C, so B is the point of concurrency of the lines containing the altitudes. Therefore, B is the orthocenter of triangle AHB, and B also is one of the vertices of triangle ABC. So B is vertex of the main triangle and orthocenter of a sub-triangle. The same logic can be used to show that the orthocenters of the other two sub-triangles will lie other two vertices of triangle ABC.
---
This is an interesting exploration, for the investigation of the orthocenters of the subtriangles led to interesting results. This exploration with Geometer's SketchPad would enhance the instruction of triangle centers, for students can discover relationships that normally would not surface.