

Assignment 9: Pedal Triangles
Presented by: Amanda Oudi
For this write-up, I will take
a look at what happens if the pedal point P is located at the different centers
of triangle ABC. Using GSP, I can easily explore how the location of the pedal
point P varies as the triangle centers vary, and draw a few mathematical
conclusions.
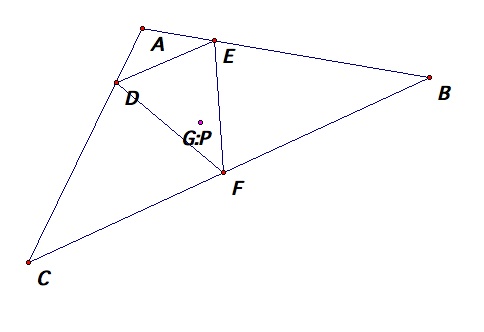
Let’s begin by making a few
initial conjectures. We know that the centroid, G, of a triangle is the point
in which the the medians of a triangle intersect. As the shape of the triangle
varies (acute, right, and obtuse), the centroid always remains inside the
triangle.This makes sense since the centroid is referred to as the balance
point of the triangle. With this in mind, I will make the guess that if the
pedal point P is located at the centroid of the triangle, then the point will
also remain inside the triangle. So, the vertices of the pedal triangle will
lie on the sides of the original triangle ABC. Using GSP, I explored this
conjecture and found that the vertices of the pedal triangle were on the sides
of triangle ABC and that the pedal point always remained on the inside of the
triangle. See GSP sketch for exploration.
Case ii: What if the pedal point P is the incenter of
the triangle ABC.
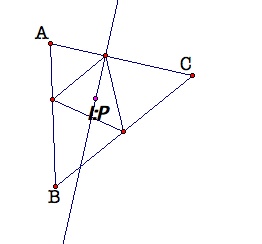
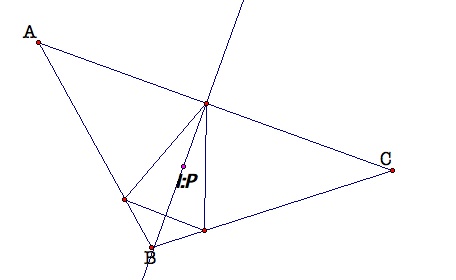
Again, let’s make a few
intial conjectures. We know that the incenter, I, is the point in which the
angle bisectors of a triangle intersect. The incenter is always found inside a
triangle. So again, I predict that the pedal point, P, will also lie within the
triangle, and that the vertices of the pedal triangle lie on the sides of the
original triangle ABC. Using GSP, I explored this conjecture and found that
this was indeed the case. See GSP Sketch for exploration.
Case iii: What if the pedal point P is the orthocenter
of the triangle ABC.
What’s the prediction this
time? We know that the orthocenter, H, is the point in which the lines
containing the altitudes of a triangle intersect. Unlike the centroid and
incenter, the location of the orthocenter is not restricted to the inside of a
triangle. Instead, the location of the orthocenter varies as the shape of the
triangle varies. When the triangle is acute, the orthocenter is located inside
the triangle. So, I expect that the pedal triangle will be located inside the
triangle, as well as pedal point P. When the triangle is right, the orthocenter
is located on the vertex of the right angle. I predict that the pedal triangle
and point would lie inside the original triangle ABC. Lastly, when the triangle
is obtuse, the orthocenter is located outside the triangle. So, I expect the
pedal triangle will be located outside the triangle, as well as the pedal
point.
Using GSP, I explored this
conjecture and noted the following results:
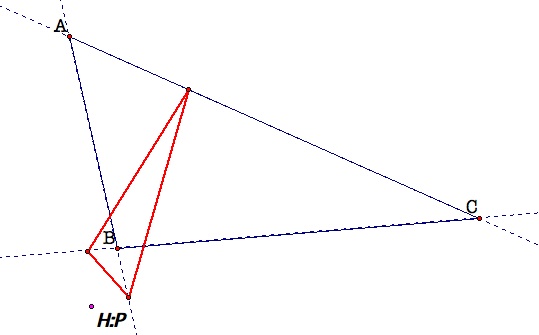
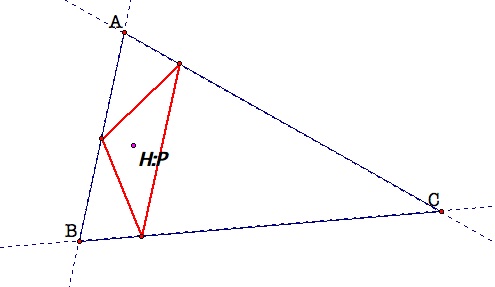
When triangle ABC was an
acute triangle, the pedal point and triangle was inside triangle ABC. The pedal
point P was located at the orthocenter of an acute triangle. When triangle ABC
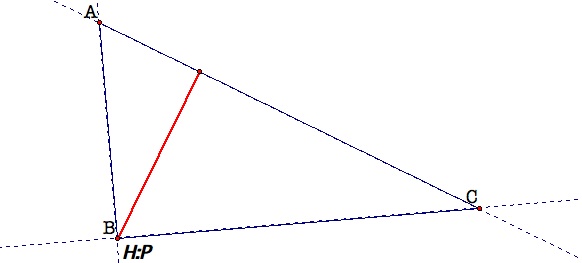
was a right triangle, the pedal triangle did not exist! That was surprising!
Instead, a segment was formed and the pedal point P was located at the vertex
of the right angle, same as the orthocenter of a right triangle. See GSP sketch
for exploration.
I predict somewhat similar results when pedal point P is the circumcenter of triangle ABC. Try it yourself!
What a thought provoking
exploration. The mysterious question is why when the pedal triangle in case
iii. is simply a line segment. Conjectures? Proofs? I need to think about this
some and see I can come up with anything. This would be a good exploration to
enhance the unit relating to triangle centerds. While triangle centers is part of the mathematics curriculum, not enough emphasis or explorations are done with these centers. The focus is more on the construction of 4 basic triangle centers: centroid, incenter, orthocenter, and circumcenter, rather than the interesting characteristics and relationships among the triangle centers.