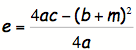Presented By:

Dana TeCroney

The challenge in this assignment is to find two functions f(x) and g(x) such that their product:

h(x) = f(x)*g(x)

is tangent at two distinct points.

Not only will I give an example to solve the given question, but this method will be generalized to show that when give h(x) = ax² +bx +c, there are an infinite number of lines that could produce such a quadratic.

To begin, consider the polynomial h(x) = -x² + 6x - 5

Choose a slope for f(x), say m = 3. Because of the symmetry of parabolas, the slope of g(x) will be m = -3. Now, values for the constants in f(x) and g(x) must be determined.

Consider f(x) = 3x + d

As 'd' changes, the line shifts such that sometimes f(x) and h(x) intersect in two places, sometimes in one place, and at other times not at all. For a graph of this, press HERE.

We are concerned with where f(x) and h(x) are tangent, i.e. intersect once. To find this value we want to know where h(x) = f(x) at only one point, or, where h(x) - f(x) = 0 has only one root. To see the effects of changing ‘d’ press HERE. The graph would look like this:

Another way to look at this is when the discriminate of h(x) – f(x) = 0:

h(x) – f(x) = -x² + 6x – 5 – (3x + d) =0

= -x² + 3x + (-5 - d) = 0

The discriminate would be equal to zero where

3² – 4(-1)(-5 - d) = 0

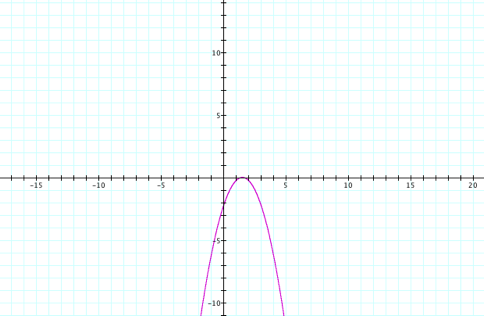
Or, when d = -11/4

Therefore, f(x) = 3x – 11/4

Here is a graph of f(x) (red) and h(x) (purple):

The same process can be followed to find g(x). Remember, the slope of g(x) was -3:

g(x) = -3x + e

What should our ‘e’ be?

Again we want h(x) and g(x) to be tangent, so we want the discriminate of h(x)- g(x) = 0:

-x² + 6x – 5 – (-3x + e) = 0

=> -x² + 9x + (-3 – e) = 0

The discriminate of this would be equal to zero where:

9² – 4(-1)(-3 – e) = 0

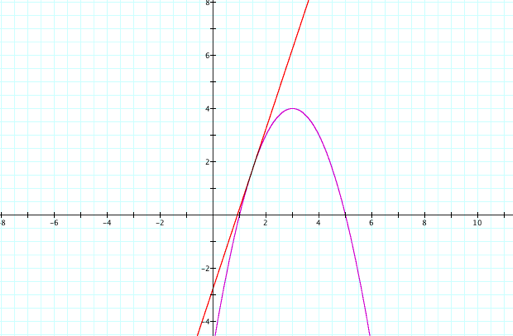
Or where e = 61/4

Therefore g(x) = -3x + 61/4

Here is the resulting graph:

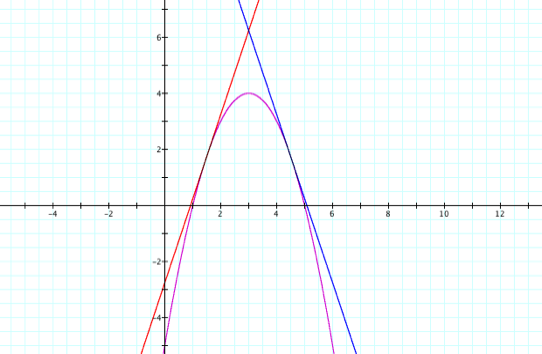
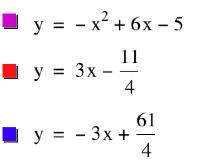
In general, consider a quadratic of the form h(x) = ax² + bx + c. Choose an arbitrary slope for f(x), say m. The slope for g(x) must be –m.

h(x) = ax² + bx + c

f(x) = mx + d

g(x) = -mx + e

To find values for constants d and e, one must find where h(x) = f(x) and where h(x) = g(x) tangentially.

In other words the discriminates of the function h(x) – f(x) = 0 is zero and where the discriminate h(x) – g(x) = 0 is zero.