OTP (Outside the Parameter)

Presented by

Dana TeCroney

 

The purpose of this investigation is to explore parametric equations using the program Graphing Calculator.  Consider the equation .  With many other graphing technologies such as the TI calculators, this equation cannot be graphed (as is, parametric equations are necessary), but can with Graphing Calculator. 

 

 

How else could you deal with an equation like this? 

 

If we wrote this in parametric form would things change?  Well, let's see shall weÉ

 

Let y = tx, where t is our parameter.  Now, substituting for t, we obtain.

 

x3 + t3y3 = 3x2

With a little algebra, it can be shown that:

 

,

 

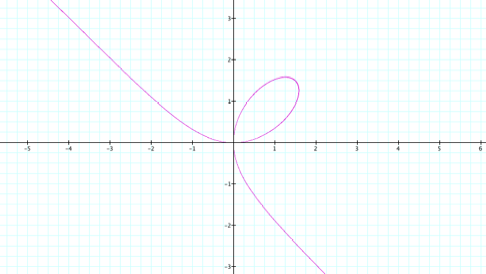
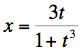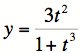
Now things get interesting when we begin to graph this parametrically with different ranges for t, start with t = 0 .. 1.  In the following graphs, the pink is the original graph of  and the blue graphs are the parametric equations.

 

 

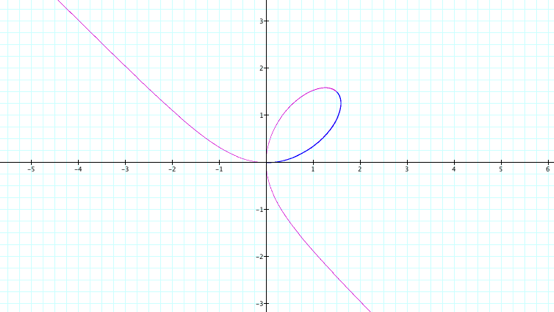
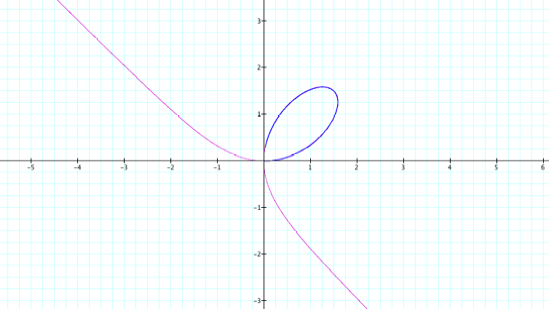
Obviously this range isn't good enough, so try t = 0 É 10

 

 

t = 0 É 100?

 

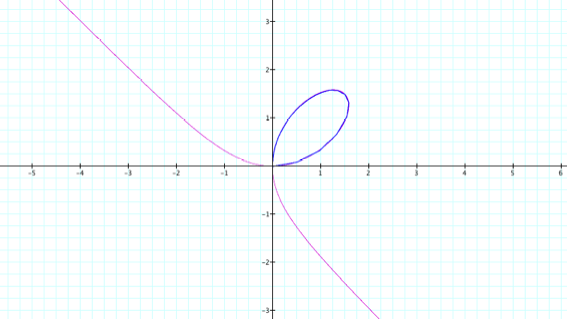
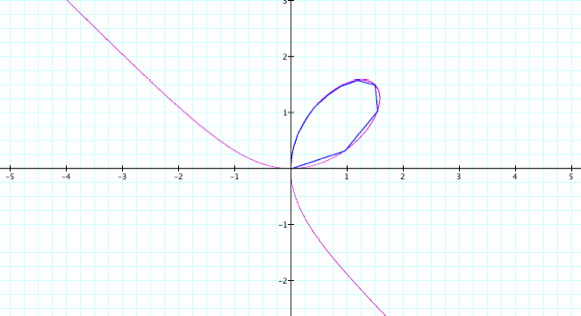
If you look closely, this is actually a worse approximation of the original graph, to illustrate the point, try t = 0 É 200.  You can see how the approximation is becoming more rigid and less smooth.

 

 

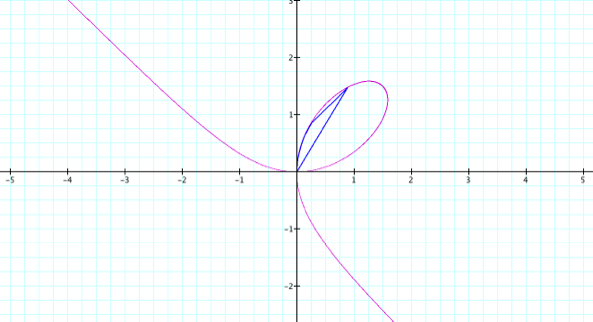
When t = 0 É 1000, the approximation isnÕt even close as shown below.

 

As shown in the graphs above the best upper bound we have tried is t = 10, however we have only covered the loop of the original graph.  To cover the rest, we need to consider negative values of t, however, there is a problem: domains.  In the original equation , the domain consists of all real numbers, however, , , has a domain restriction of t not equaling -1.  So, can we approximate the entire graph with a t value less than -1?  The graph below shows t = -.999 É 10.

 

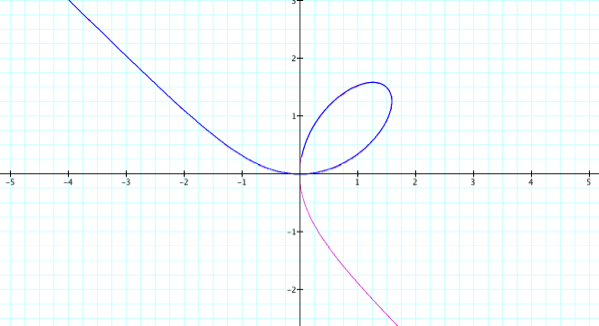
As it turns out, t = -10 É 10 gives us an approximation for the whole graph, but there is an extra line where the slant asymptote isÉ

 

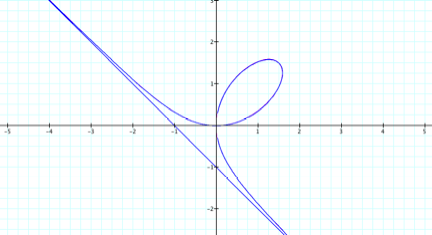
This illustrates one of the limitations of technology.  When graphing technologies are given parametric equations, they evaluate a given number of points and then connect these points.  So why the line?  Consider the following.

   =                    =   

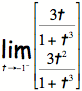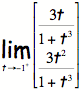As you can see, as t gets really close to -1, the points are far off in the second and forth quadrant depending on whether you are approaching from the left or the right.  When you put this all together, the technology connects these points and hence the line, despite the fact that the line (asymptote) isnÕt part of the graph.