
Presented by: Dana TeCroney
Assignment 2
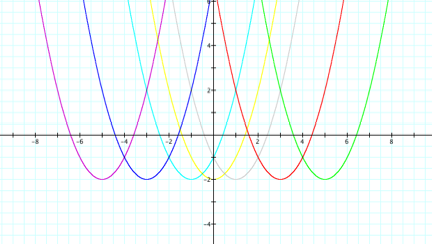
Classification of y = (x – d)2 – 2
The
purpose of this assignment is to discuss the function y = (x – d)2
– 2 as d varies.
Specifically, for different values of d, we wish to discover if the
shape of the graph is altered, and if the position changes.
Consider
the following graph:
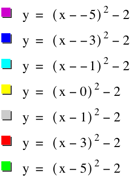
To
see an animation of this graph as d varies from -5 to 5 and back again, press me.
If
you would like to control the value of d, press
me.
As
you can see from the graph above, the shape of the graph is unaffected by the
different values of d, however the position does change. When d = 0, y = (x – 0)2
– 2 is a parabola that opens up with the vertex at (0,-2). As d decreases, the parabola shifts to
the left. As d increases, the
parabola shifts to the right, with the vertex in all cases at (d,-2). This follows directly from the vertex
form of a parabola y =
(x – h)2 + k where (h,k) is the vertex.