Presented by

Dana TeCroney

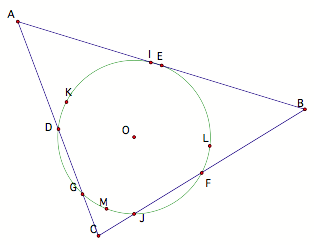
The Nine-Point circle for any triangle passes through the three mid-points of the sides, the three feet of the altitudes, and the three mid-points of the segments from the respective vertices to orthocenter. The objective of the following is to construct the nine points, locate the center (N) and construct the nine point circle.

First, begin with an arbitrary triangle ABC.

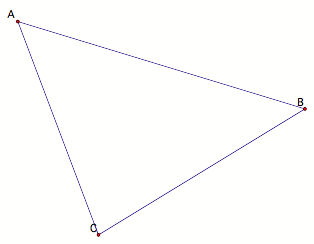
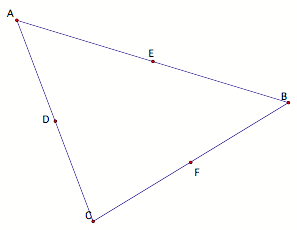
If the nine point circle is to pass through the midpoints of the sides of the triangle, locate them next, call them D, E, and F.

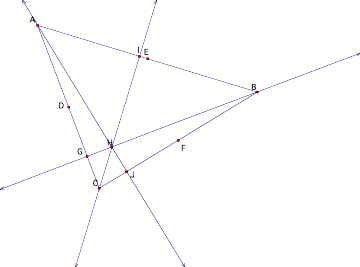
Next we need the three feet of the altitudes, which are the lines pass through a vertex and perpendicular to the opposite side. Call them G, I, and J. The point where the altitudes are concurrent is called the orthocenter and by convention is labeled H.

We will need the orthocenter next if we are to construct three mid-points of the segments from the respective vertices to orthocenter. Call them K, L, and M.

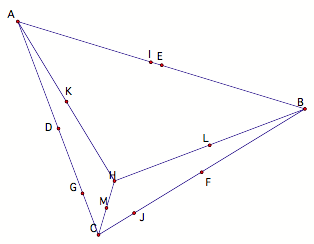
One way to find the center of the nine point circle (O) is to find the midpoint f the segment that connects the orthocenter (H) and the circumcenter (N), which is the intersection point of the perpendicular bisectors of each side of the original triangle.

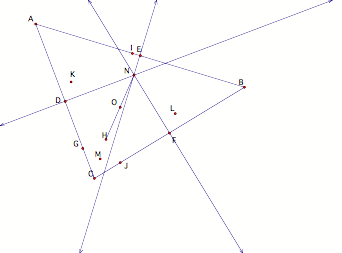
The moment of triumph…

If you would like to move this nine point circle around to see how it looks for different triangles, press HERE.