Presented by

Dana TeCroney

The purpose of this investigation is to explore tangent circles. First I will discuss the construction of a certain type of tangent circles, then I will argue that the locus of the center of the constructed circle is either an ellipse or a hyperbola.

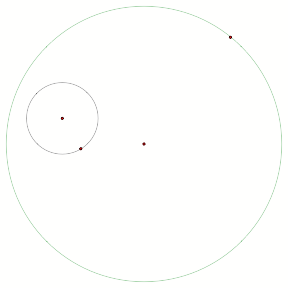
First consider a circle within a circle.

The type of tangent circle I wish to regard is one who is tangent to the outside of the black circle and also tangent to the green circle. To construct such a circle choose an arbitrary point on the green circle and draw in the radius. Mark off a distance equal to the radius of the black circle.

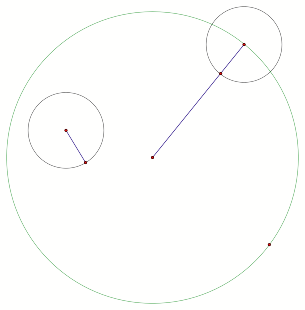
Connect points A and C (below), this will be the base of an isosceles triangle. To make this isosceles triangle, draw in the perpendicular bisector of segment AC to find point B on the radius of the green circle.

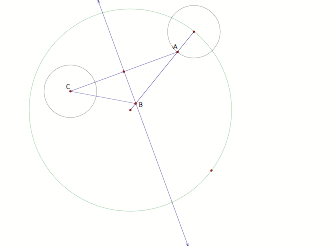
Now using segment BD as a radius, construct the red tangent circle. This will be tangent to the outside of the black circle since the radii of the black circles is the same and segment AD would be the same as segment BC the radius of circle C.

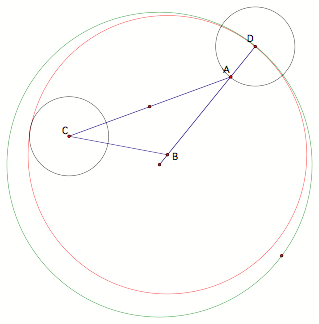
The tangent circle has now been constructed, of you would like to see how these circles move in relation to one another, press HERE.

Now consider the locus of the center of the red tangent circle. This will be done in three cases, if the black circle is inside the green circle, if the black and green circles intersect, and if the black circle is outside the green circle.

CASE I: The black circle is inside the green circle.

In the following sketch, the purple shape is the trace of the center of the tangent circle (B), which appears to be an ellipse with the centers of the red and black circles as the foci. Is it though?

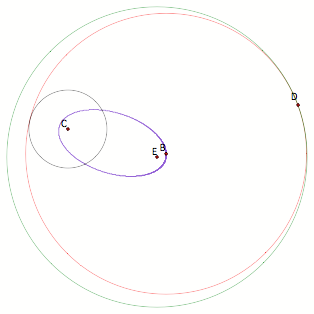
For this to be an ellipse, there needs to be a constant sum of the distances mBE and mBC. In fact it will be since ED is constant and mED – mAD = mEB + mBA, but mBA and mBC are the same since the triangle is isosceles.

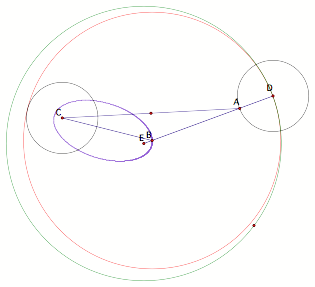
CASE II: The black and green circles intersect.

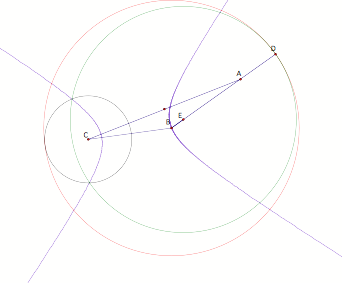
To show that the purple trace is a hyperbola, it must be shown that mCB – mBE = cnst. Notice that ED is the radius of the green circle, which we are holding constant. The only thing we are changing is the position of D. From an earlier construction, it was shown that mCB = mAB. This implies that mBD = mAB +mAD, subtracting mAD (distance equivalent to the radius of circle C) from both sides yields mCB = mBE + mEA, or, mCB – mBE = mEA. Of course, mEA is a constants since we are not changing the distance in either radius.

CASE III: The black circle is outside the green circle.

To show the purple trace is a hyperbola, the exact same argument as CASE II can be used.

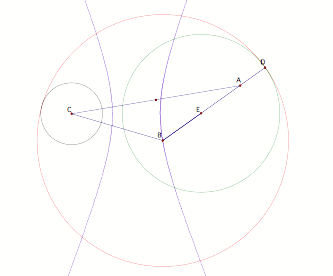
If you would like to experiment with these circles and the locus of the set of points traced by the center of the tangent circle, press HERE. To change position of the black circle, be sure to select the circle (not the center) and move it.