
_______________________________________________________________________________________________________
Cryptorithms
Presented by:
Dana TeCroney
Cryptorithms are puzzles where a single digit number replaces
every letter, and the challenge is to find the corresponding numbers. For example:

These
puzzles test your knowledge of addition properties (or other arithmetic
operations), often with a not so hidden messageÉ
One
way to solve this problem is to begin with the left most digit in the
answer. In this case, L = 1
because the most that could be grouped (when the digits in a column sum to 10
or more) from the ten thousands column (the B column) is 1. At this step, you can also conclude
that B = 9 and O = 0.
Consider:
If
E + C were the next two larges available digits, 8 + 7 = 16, and if we add 2
(the largest number that could be grouped from a previous column) then the sum
is 18 < 20, which means B = 9 to produce L = 1. Furthermore, O = 0.
Now
lets fill in our progress (notice I put in the group from the thousands
column):
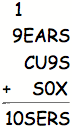
B = 1; L = 1; O = 0
At
this point, the problem gets interesting because the solution is not unique
(yes, sometimes there is more than one possible answer!). There are a lot of SÕs in the problem,
so that might be a good place to go next.
Lets look at some different possibilities for the oneÕs column and keep
in mind, S + S + X = S, so S + X = 10.
Try
I: S = 7; X = 3
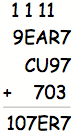
If
this were the case, the E + C must be 16 in order to add a group of 10 to the
ten thousands place (the 9 and 1).
This canÕt happen though because the largest two available numbers are 8
and 6, 8 + 6 = 14. Even if one
were added to this, we still couldnÕt get 16É
Try
II: S = 6; X =4
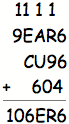
Here,
E + C > 10 because earlier we showed that a group of 10 went with the
9. In fact E + C = 15. If E = 8, the A + U = 10, but this
canÕt happen because the available digits would be 5, 3, and 2, no two of which
sum to ten. So what if E = 7? Again this wonÕt work for similar
reasons.
Try
III: S = 2; X = 8
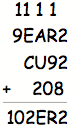
In
this case, E + C = 11. LetÕs try E
= 4 and C = 7. This implies that A
+ U = 11. One possibility is A = 5 and U = 6, leaving R = 4.
B = 9 C
= 7 S
= 2 L = 1
E = 4 U
= 6 O
= 0
O = 0
A = 5 B
= 9 X
= 8 S = 2
R = 4 S
= 2 S
= 2 E = 4
S = 2 R = 4
S = 2
Here
is one answer, can you find any more???
If
you would like to try some cryptorithms, press here.
Possible
extensions:
Finding
more answers. On the linked page,
there are crytorithms using different operations, and these could be
explored. These could be used in a
classroom as an introduction to logic that may interest students. There are many conditional situations
that result in these problems and force students to consider a number of
different cases.