Distance
Survey Problem
In conducting a land survey, the following problem arose. There
were two points A and B along a road and points B and D off the road along the respective
perpendiculars to the road at A and B. There were buildings on the property
that prevented direct measurement of the distances along BD and AC.
Measurements, however, could be made for AD, BC, and AB as follows:
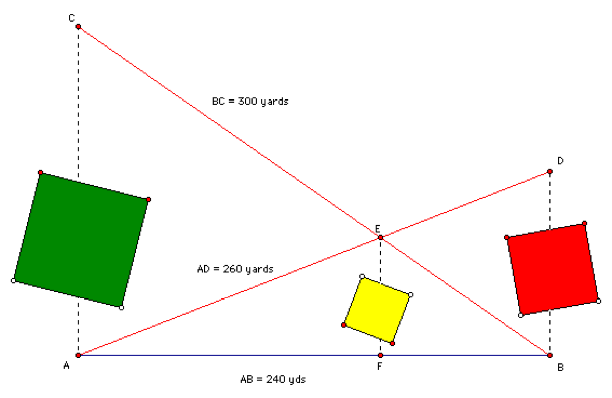
AB = 240 yards
AD = 260 yards
BC = 300 yards
A light pole is to be installed at point E, the intersection of CB
and AD. How far will the pole be from the road. That is what is the distance
EF? Again, an existing building blocks direct measurement.
Method
I: Similar triangles
Consider
the following diagram
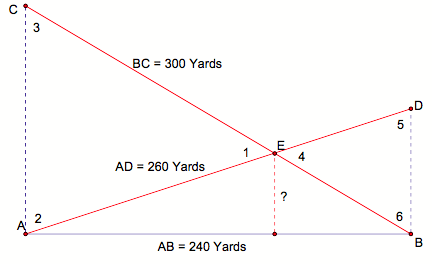
Notice,
∆ACE and ∆DBE are similar triangles since all the angles are congruent. Angles 1 and 4 are vertical angles, and
(3 and 6) and (2 and 5) are alternate interior angles with parallel lines CA
and DB cut by transversals CB and AD.
What
is the ratio between ∆ACE and ∆DBE?
One
way to find this ratio is to find the length of AC and DB. The Pythagorean Theorem works nicely
here with ∆ABC and ∆ADB.
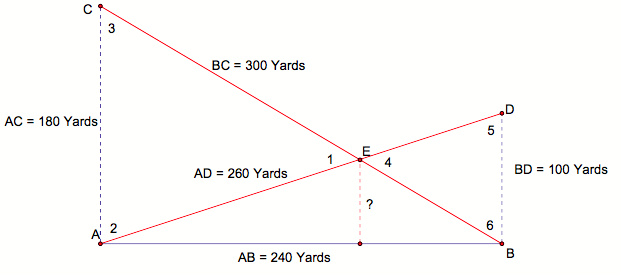
From
this result, it can be determined that ∆ACE is ![]() the size of
∆DBE.
the size of
∆DBE.
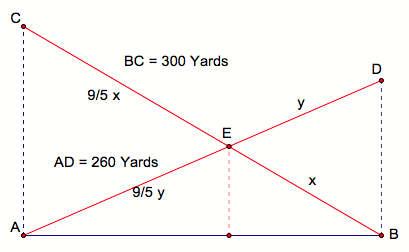
Using
this ratio, the length of AE and BE can be determined:
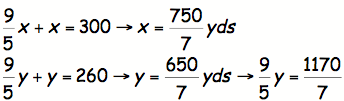
Now
consider ![]() :
:
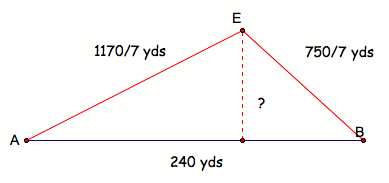
The
area of this triangle can be found in two ways, using A = ½base*height
and Heron's formula:
Heron's
Formula: 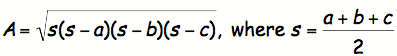
Using
this formula, the area was found to be ![]()
Using
the formula A = ½base*height, the height (distance from the light pole
to the road) can be calculated to be ![]() .
.
Possible
Extensions:
Interestingly
enough, this result could have been found in a much simpler way if you know a
bit about harmonic means. How does
this problem relate to harmonic means?