Bouncing Purple Dinosaur

Presented By

Dana TeCroney

Barney is in the triangular room shown here. He walks from a point, D, on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC (the line/wall he just came from). When he reaches AC, he turns and walks parallel to AB. What I wish to prove is that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point?

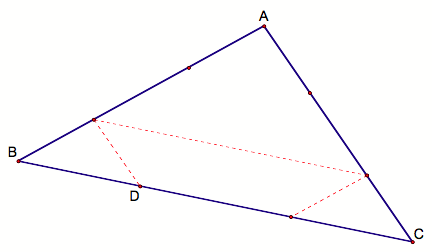
Well, first look at the entire situation. The path of travel is shown below by the red lines.

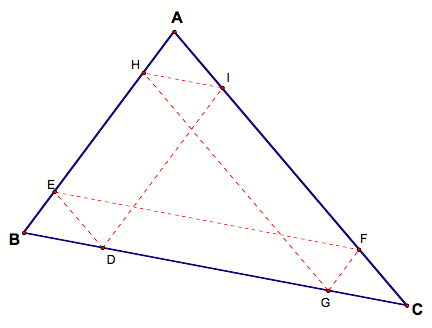
By construction, there are a plethora of parallel lines. In the picture below, all the blue lines are parallel, all the green lines and parallel, as are all the brown lines. Note that all the lines that are not parallel act as transversals.

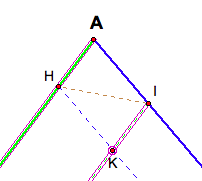
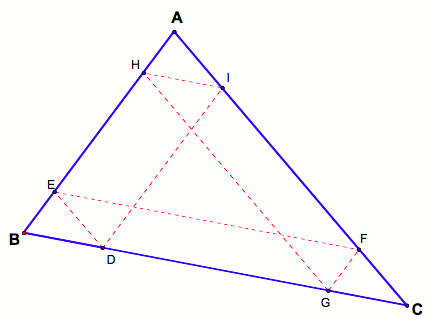
First, I will argue that the triangles formed in the corners are congruent. Consider one corner. In the figure below, angle EBD is congruent to angle JDG (G is along the side BC) since they are corresponding angles. Angle JDG is also congruent to angle EJD because they are alternate interior angles, and hence, angle EBD and angle EJD are congruent.

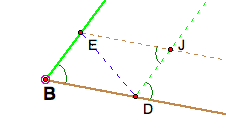
Angles EDB and angle DEJ are also alternate interior angles and hence congruent. Now since ∆EDB and ∆DEJ share side ED, they are congruent by an angle-angle-side argument.

A similar argument can be made for the other two corners of the triangle.

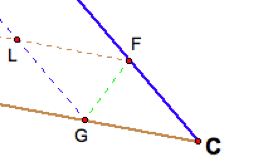
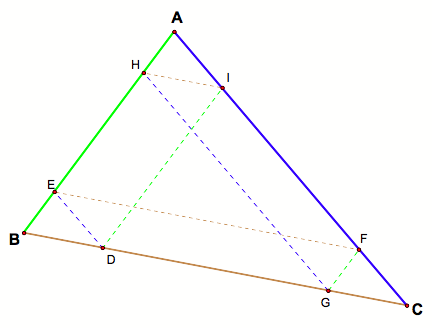
Another set of situations created by the parallel line is the formation of parallelograms. In the figure below, the opposite sides are parallel, and hence the shaded figure is a parallelogram. A result that follows is that side DE is congruent to CF.

Why is this important? It provides the missing link to show the all the triangles in the corners are congruent. In the figure below, angles EJD and LFG are congruent because they are corresponding one another (parallel lines FG and ID cut by transversal EF). Similarly, angles JED and FLG are congruent (parallel linseed and HG cut by transversal EF), and hence, ∆EJD is congruent to ∆LFG by a side-angle-angle argument.

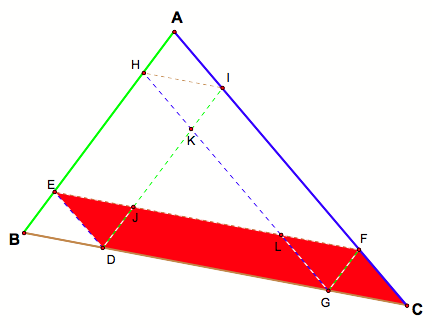
The transitive property then gives us the fact that ∆EBD is congruent to ∆FGC. This implies that side BD is congruent to side CG.

A similar argument can be made to show that the shaded orange region below is a parallelogram and hence side CG is congruent to HI. Side HI is also congruent to BD for the same reasons.

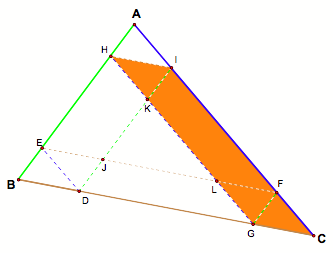
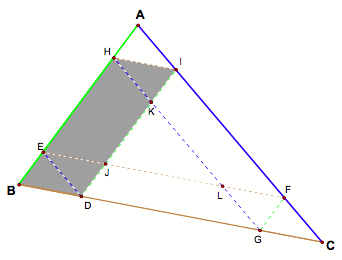
The moment of triumph,

Remember, Barney walks from a point, D, on BC, parallel to AC. When he reaches AB, he turns and walks parallel to BC (the line/wall he just came from). When he reaches AC, he turns and walks parallel to AB. Barney will then walk parallel to AC and reach AB at point H, where he turns and walks to I. From there he turns and walks until he hits BC. Since he's walking parallel to AB, his finishing distance will be the same as the distance from H to I (side HI). In the arguments above, it was shown that HI is congruent to BD, which was the starting distance, hence Bouncing Barney will finish in the same place that he started.

If you would like to experiment with Bouncing Barney, PRESS HERE. What do you think would happen if side BC were extended to be a line, so D is outside the triangle? Interestingly enough, the result still holds, to see it, PRESS HERE.